
| b | a |
科目:初中数学 来源: 题型:
| b |
| a |
 鸡蛋型”的椭球.已知半径为a的球的体积为
鸡蛋型”的椭球.已知半径为a的球的体积为| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:填空题
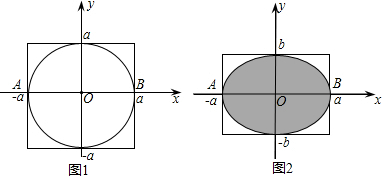
(1)善于思考的小迪发现:半径为 ,圆心在原点的圆(如图1),如果固定直径
,圆心在原点的圆(如图1),如果固定直径 ,把圆内的所有与
,把圆内的所有与 轴平行的弦都压缩到原来的
轴平行的弦都压缩到原来的 倍,就得到一种新的图形
倍,就得到一种新的图形 椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .

(2)(本小题为选做题,做对另加3分,但全卷满分不超过150分)小迪把图2的椭圆绕 轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为
轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为 的球的体积为
的球的体积为 ,则此椭球的体积为 .
,则此椭球的体积为 .
查看答案和解析>>
科目:初中数学 来源:第25章《图形的变换》好题集(07):25.3 轴对称变换(解析版) 题型:填空题
 倍,就得到一种新的图形-椭圆(如图2).她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”、“化曲为直,以直代曲”的方法,正确地求出了椭圆的面积,她求得的结果为 ;
倍,就得到一种新的图形-椭圆(如图2).她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”、“化曲为直,以直代曲”的方法,正确地求出了椭圆的面积,她求得的结果为 ; πa3,则此椭球的体积为 .
πa3,则此椭球的体积为 .
查看答案和解析>>
科目:初中数学 来源:2012年10月中考数学模拟试卷(10)(解析版) 题型:填空题
 倍,就得到一种新的图形------椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
倍,就得到一种新的图形------椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com