
 如图,OA⊥OB,等腰三角形△MNC的顶点N、C在OA、OB上,∠M=90°,将△MNC绕点C顺时针旋转75°,点M的对应点D恰好落在OB上,则$\frac{OC}{CD}$的值为$\frac{\sqrt{2}}{2}$.
如图,OA⊥OB,等腰三角形△MNC的顶点N、C在OA、OB上,∠M=90°,将△MNC绕点C顺时针旋转75°,点M的对应点D恰好落在OB上,则$\frac{OC}{CD}$的值为$\frac{\sqrt{2}}{2}$. 分析 由等腰直角三角形的性质和勾股定理得出∠MNC=∠MCN=45°,CM=$\frac{\sqrt{2}}{2}$CN,由旋转的性质得:∠DCE=∠DCE=∠MCN=45°,CD=CM,∠ECN=75°,求出∠DCN=120°,得出∠OCN=60°,由直角三角形的性质求出∠ONC=30°,OC=$\frac{1}{2}$CN,即可得出答案.
解答 解:∵等腰三角形△MNC的顶点N、C在OA、OB上,∠M=90°,
∴∠MNC=∠MCN=45°,CM=$\frac{\sqrt{2}}{2}$CN,
由旋转的性质得:∠DCE=∠DCE=∠MCN=45°,CD=CM=$\frac{\sqrt{2}}{2}$CN,∠ECN=75°,
∴∠DCN=45°+75°=120°,
∴∠OCN=60°,
∵OA⊥OB,
∴∠ONC=30°,
∴OC=$\frac{1}{2}$CN,
∴$\frac{OC}{CD}$=$\frac{\frac{1}{2}CN}{\frac{\sqrt{2}}{2}CN}$=$\frac{\sqrt{2}}{2}$;
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了旋转的性质、等腰直角三角形的性质、勾股定理、含30°的直角三角形的性质等知识;熟练掌握旋转的性质和等腰直角三角形的性质,求出∠ONC=30°是解决问题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 2x2•3x3=6x3 | B. | 2x2+3x3=5x5 | ||
| C. | -12a3b4÷2a3b2=-6b2 | D. | $\frac{5}{4}$xn•$\frac{2}{5}$xm=$\frac{1}{2}$xmn |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 138×103米 | B. | 13.8×104米 | C. | 1.38×105米 | D. | 1.38×103米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
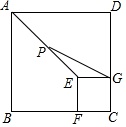 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为$\sqrt{5}$.
如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象是一条直线 | B. | 它的图象分布在第一、三象限 | ||
| C. | 点(-1,-5)在它的图象上 | D. | 当x>0时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
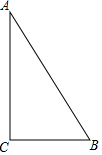 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com