练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
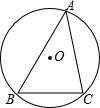
    10．如图，⊙O是△ABC的外接圆，⊙O的半径为4，∠A=45°，则$\widehat{BC}$的长是（　　）
    A．4πB．8πC．2πD．1

    分析 连接OB、OC，根据圆周角定理求出∠BOC，利用弧长公式计算即可．

    解答 解：连接OB、OC，
    由圆周角定理得，∠BOC=2∠A=90°，
    ∴$\widehat{BC}$的长=$\frac{90π×4}{180}$=2π，
    故选：C．

    点评 本题考查的是三角形的外接圆和外心的概念和性质，掌握圆周角定理、弧长公式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．下列命题是假命题的是（　　）
    A．两组对边分别平行的四边形是平行四边形
    B．两条对角线相等的平行四边形是矩形
    C．两条对角线互相垂直的平行四边形是菱形
    D．两条对角线垂直且相等的四边形是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．a、b是两个连续整数，若a＜$\sqrt{3}$＜b，则a、b分别是（　　）
    A．0、1B．1、2C．2、3D．3、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，PA、PB是⊙O的两条切线，A、B是切点，PA=$\sqrt{3}$OA，阴影部分的面积为6π，则⊙O的半径长为3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，⊙O的两条弦AB、CD相交于点P，∠APC=45°，若⊙O的半径为4，则扇形AOC与扇形DOB面积（图中阴影部分）的和为4π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）计算：2cos45°-$\sqrt{8}$+（2018-$\sqrt{2017}$）0
    （2）化简：1-$\frac{a-1}{a}$÷$\frac{{a}^{2}-1}{{a}^{2}+2a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知P1（x1，y1），P2（x2，y2）是一次函数y=-$\frac{1}{3}$x+2图象上的两点，下列判断中，正确的是（　　）
    A．y1＞y2B．y1＜y2C．当x1＜x2时，y1＜y2D．当x1＜x2时，y1＞y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

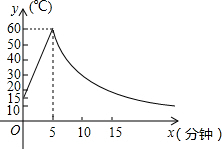    19．制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
    （1）求出将材料加热时，y与x的函数关系式；
    （2）求出停止加热进行操作时，y与x的函数关系式；
    （3）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么操作时间是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．不等式组$\left\{\begin{array}{l}{2x＜5}\\{x-2＜0}\end{array}\right.$的解集是x＜2．

    查看答案和解析>>

    同步练习册答案