练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图1所示的是一个长方形纸带，∠DEF=25°，将纸带沿EF折叠成图2，则图2中的∠BGE的度数是50°．

    分析 根据折叠的性质求出∠FEG=∠DEF=25°，根据平行线的性质求出即可．

    解答 解：∵∠DEF=25°，将纸带沿EF折叠成图2，
    ∴∠FEG=∠DEF=20°，
    ∵AD∥BC，
    ∴∠EGB=25°+25°=50°．
    故答案为：50°．

    点评 本题考查了平行线的性质，折叠的性质的应用，能求出∠FEG=∠DEF=25°和求出∠EGB=25°+25°是解此题的关键，注意：两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．在直角坐标中，点P（2，-3）所在的象限是（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．函数y=2x和y=ax+4的图象相交于点A（m，3），则方程2x=ax+4的解为x=1.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如果$\sqrt{\frac{x}{x-3}}=\frac{\sqrt{x}}{\sqrt{x-3}}$成立，那么（　　）
    A．x≥3B．0≤x≤3C．x≥0D．x＞3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

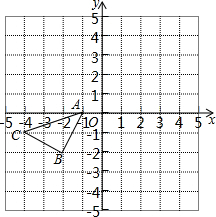    2．如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：
    （1）以A点为旋转中心，将△ABC绕点A顺时针旋转90°得△AB1C1，画出△AB1C1．
    （2）作出△ABC关于坐标原点O成中心对称的△A2B2C2．
    （3）作出点C关于x轴的对称点P．若点P向右平移x个单位长度后落在△A2B2C2的内部（不含落在△A2B2C2的边上），请直接写出x的取值范围．
    （提醒：每个小正方形边长为1个单位长度）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

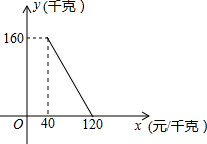    12．某商店以40元/千克的单价新进一批茶叶，经调查发现，在一段时间内，销售量y（千克）与销售x（元/千克）之间函数关系如图所示．
    （1）求y与x函数关系式；
    （2）商店想在销售成本不超过3800元的情况下，使销售利润达到3000元，销售单价应定为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，在⊙O中，∠C=30°，AB=2cm，则弧AB的长等于$\frac{2π}{3}$．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

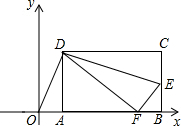    16．如图，矩形ABCD的顶点AB在x轴上，点D的坐标为（3，4），点E在边BC上，△CDE沿DE翻折后点C恰好落在x轴上点F处，若△ODF为等腰三角形，点C的坐标为（8，4）或（3$+2\sqrt{5}$，4）或（$\frac{43}{6}$，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图1，S是矩形ABCD的AD边上一点，点E以每秒kcm的速度沿折线BS-SD-DC匀速运动，同时点F从点C出发点，以每秒1cm的速度沿边CB匀速运动并且点F运动到点B时点E也运动到点C．动点E，F同时停止运动．设点E，F出发t秒时，△EBF的面积为ycm2．已知y与t的函数图象如图2所示．其中曲线OM，NP为两段抛物线，MN为线段．则下列说法：
    ①点E运动到点S时，用了2.5秒，运动到点D时共用了4秒
    ②矩形ABCD的两邻边长为BC=6cm，CD=4cm；
    ③sin∠ABS=$\frac{\sqrt{3}}{2}$；
    ④点E的运动速度为每秒2cm．其中正确的是（　　）
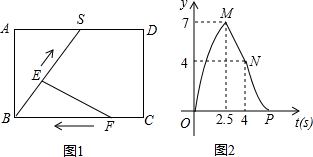
    A．①②③B．①③④C．①②④D．②③④

    查看答案和解析>>

    同步练习册答案