
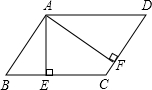
 如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$.
如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$. 分析 要求平行四边形的周长就要先求出AB、AD的长,利用平行四边形的性质和勾股定理即可求出.
解答 解:∵∠EAF=45°,
∴∠C=360°-∠AEC-∠AFC-∠EAF=135°,
∴∠B=∠D=180°-∠C=45°,
则AE=BE,AF=DF,
设AE=x,则AF=2-x,
在Rt△ABE中,根据勾股定理可得,AB=$\sqrt{2}$x,
同理可得AD=$\sqrt{2}$(2-x).
则平行四边形ABCD的周长是2(AB+AD)=2[$\sqrt{2}$x+$\sqrt{2}$(2-x)]=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查了平行四边形的性质,解题关键是利用平行四边形的性质结合等角对等边、勾股定理来解决有关的计算和证明.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
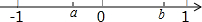 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2ab | B. | +2ab | C. | +4ab | D. | -4ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
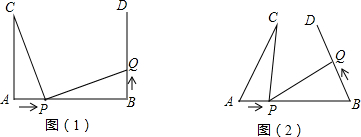
 如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com