
【题目】如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是( ) 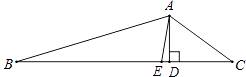
A.10°
B.12°
C.15°
D.18°
【答案】A
【解析】解:∵AD⊥BC,∠C=36°, ∴∠CAD=90°﹣36°=54°,
∵AE是△ABC的角平分线,∠BAC=128°,
∴∠CAE= ![]() ∠BAC=
∠BAC= ![]() ×128°=64°,
×128°=64°,
∴∠DAE=∠CAE﹣∠CAD=64°﹣54°=10°.
故选A.
【考点精析】通过灵活运用三角形的“三线”和三角形的内角和外角,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,

(1)按此规律,图案⑦需____根火柴棒;第n个图案需____根火柴棒.
(2)用2018根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=﹣(x﹣2)2+ ![]() 的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用下面的备用图画出图象来分析).
的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用下面的备用图画出图象来分析). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=( )
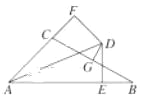
A. 6 B. 3 C. 2 D. 1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEO的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC是任意一条射线,OD,OE分别是∠AOC和∠BOC的平分线,
(1)图中∠BOD的补角是_______________;∠BOE的余角是____________________.
(2)如果∠BOE=![]() ∠AOD, 求∠BOE的度数。
∠AOD, 求∠BOE的度数。
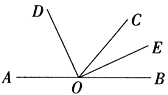
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示. 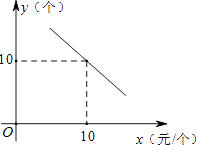
(1)求此一次函数的关系式;
(2)现批发市场进行促销活动,凭会员卡(240元/张)在该批发市场购买所有物品均进行打折优惠,若文具店购买A、B两种文具各50个,问打折小于多少折时,采用购买会员卡的方式合算;
(3)在文具店不购买会员卡的情况下,若A种文具零售价比B种文具零售价高2元/个,求这两种文具每天的销售总利润W(元)与A种文具零售价x(元/个)之间的函数关系式,并说明当A种文具的零售价为多少时,每天的销售利润最大. (说明:本题不要求写出自变量x的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置,所转过的度数是( ) 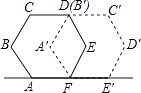
A.60°
B.72°
C.108°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
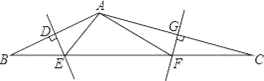
【题目】如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F.
(1)若△AEF的周长为10cm,则BC的长为______cm.
(2)若∠EAF=100°,则∠BAC______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com