
【题目】用长为6米的铝合金条制成如图所示的窗框,若窗框的高为![]() 米,窗户的透光面积为
米,窗户的透光面积为![]() 平方米(铝合金条的宽度不计).
平方米(铝合金条的宽度不计).

(1)![]() 与
与![]() 之间的函数关系式为 (不要求写自变量的取值范围);
之间的函数关系式为 (不要求写自变量的取值范围);
(2)如何安排窗框的高和宽,才能使窗户的透光面积最大?并求出此时的最大面积.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】将分别标有数字1、2、3的三张硬纸片,反面一样,现把三张硬纸片搅均反面朝上
(1)随机抽取一张,恰好是奇数的概率是多少
(2)先抽取一张作为十位数(不放回),再抽取一张作为个位数,能组成哪些两位数,将它们全部列出来,并求所取两位数大于20的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个带有进水管和出水管的容器,每分钟进、出水量都是一定的,设从某一时刻开始的4分钟内只进水,不出水,在随后的8分钟内既进水又出水,得到 时间x(分)与水量y(升)之间的关系图.(如图)
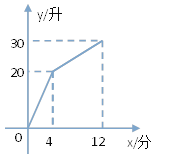
(1)每分钟进水多少?
(2)0<x≤4时,y与x的函数关系式是什么?
(3)4<x≤12时,y与x的函数关系式是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.一次函数y=![]() x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
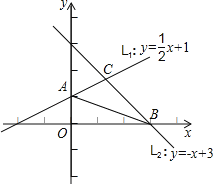
(1)求点A与点B的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱护环境越来越受到社会各界的重视,为了让学生了解环保知识,某中学组织全校![]() 名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分
名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分![]() 分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
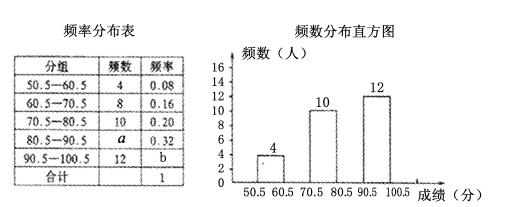
请根据以上的统计图、表解答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)成绩在![]() 分以上(不含
分以上(不含![]() 分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
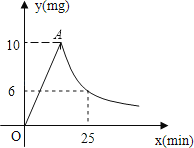
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县盛产苹果,春节期问,一外地经销商安排![]() 辆汽年装运
辆汽年装运![]() 、
、![]() 、
、![]() 三种不同品质的苹果
三种不同品质的苹果![]() 吨到外地销售,按计划
吨到外地销售,按计划![]() 辆汽年都要装满且每辆汽车只能装同一种品质的苹果,每辆汽车的运载量及每吨苹果的获利如下表:
辆汽年都要装满且每辆汽车只能装同一种品质的苹果,每辆汽车的运载量及每吨苹果的获利如下表:
苹果品种 |
|
|
|
每辆汽车运载数 |
|
|
|
每吨获利(元) |
|
|
|
(1)设装运![]() 种苹果的车辆数为
种苹果的车辆数为![]() 辆,装运
辆,装运![]() 种苹果车辆数为
种苹果车辆数为![]() 辆,据上表提供的信息,求出
辆,据上表提供的信息,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)为了减少苹果的积压,县林业局制定出台了促进销售的优惠政策,在外地经销商原有获利不变情况下,政府对外地经销商按每吨![]() 元的标准实行运费补贴若
元的标准实行运费补贴若![]() 种苹果的车辆数
种苹果的车辆数![]() 满足
满足![]() .若要使该外地经销商所获利
.若要使该外地经销商所获利![]() (元)最大,应采用哪种车辆安排方案?并求出最大利润
(元)最大,应采用哪种车辆安排方案?并求出最大利润![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
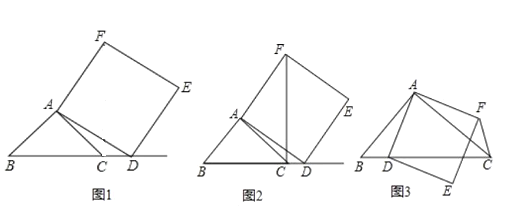
【题目】如图①,在△ABC中,![]() 为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如图②,如果AB=AC,![]() ,当点D在线段BC的延长线上时,猜想线段CF、BD的关系,并说明理由.
,当点D在线段BC的延长线上时,猜想线段CF、BD的关系,并说明理由.
(2)如图③,如果AB![]() AC,
AC,![]() 是锐角,点D在线段BC上,当
是锐角,点D在线段BC上,当![]() 时,必有CF
时,必有CF![]() BC(点C,F不重合),请先在横线上添加条件,再作证明.
BC(点C,F不重合),请先在横线上添加条件,再作证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com