
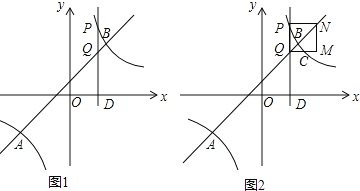
ЁОЬтФПЁПШчЭМЃЌвбжЊA(Ѓ4ЃЌn)ЁЂB(3ЃЌ4)ЪЧвЛДЮКЏЪ§y1ЃНkxЃЋbЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЕФСНИіНЛЕуЃЌЙ§ЕуD(tЃЌ0)ЃЈ0ЃМtЃМ3ЃЉзїxжсЕФДЙЯпЃЌЗжБ№НЛЫЋЧњЯп
ЕФЭМЯѓЕФСНИіНЛЕуЃЌЙ§ЕуD(tЃЌ0)ЃЈ0ЃМtЃМ3ЃЉзїxжсЕФДЙЯпЃЌЗжБ№НЛЫЋЧњЯп![]() КЭжБЯпy1ЃНkxЃЋbгкPЁЂQСНЕу
КЭжБЯпy1ЃНkxЃЋbгкPЁЂQСНЕу
(1) жБНгаДГіЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪН
(2) ЕБtЮЊКЮжЕЪБЃЌSЁїBPQЃН![]() SЁїAPQ
SЁїAPQ
(3) вдPQЮЊБпдкжБЯпPQЕФгвВрзїе§ЗНаЮPQMNЃЌЪдЫЕУїЃКБпQMгыЫЋЧњЯп![]() ЃЈxЃО0ЃЉЪМжегаНЛЕу
ЃЈxЃО0ЃЉЪМжегаНЛЕу

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉМћНтЮі
ЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЕуBЕФзјБъЧѓЕУЗДБШР§КЏЪ§НтЮіЪНЃЌдйИљОнЗДБШР§КЏЪ§ЧѓЕУЕуAЕФзјБъЃЌзюКѓИљОнД§ЖЈЯЕЪ§ЗЈЧѓЕУвЛДЮКЏЪ§НтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉЁїAPQгыЁїBPQгавЛЬѕЙЋЙВБпЃЌИљОнЭЌЕзЕФШ§НЧаЮЕФУцЛ§жЎБШЕШгкИпжЎБШЃЌСаГіЙигкtЕФЗНГЬНјааЧѓНтЃЛ
ЃЈ3ЃЉЩшжБЯпQMгыЫЋЧњЯпНЛгкCЕуЃЌИљОнЕуPЁЂQЁЂCШ§ЕуЕФзјБъЃЌгУtЕФДњЪ§ЪНБэЪОГіQM-QCЃЌдйИљОнtЕФШЁжЕЗЖЮЇХаЖЯДњЪ§ЪНЕФжЕЕФЗћКХМДПЩЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉНЋBЃЈ3ЃЌ4ЃЉДњШы![]() ЃЌЕУm=3ЁС4=12ЃЌ
ЃЌЕУm=3ЁС4=12ЃЌ
ЁрЗДБШР§КЏЪ§НтЮіЪНЮЊ![]() ЃЌ
ЃЌ
НЋAЃЈЉ4ЃЌnЃЉДњШыЗДБШР§КЏЪ§ЃЌЕУn=Љ3ЃЌ
ЁрAЃЈЉ4ЃЌЉ3ЃЉ
ЁпжБЯпy1=kx+bЙ§ЕуAКЭЕуBЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрвЛДЮКЏЪ§ЕФНтЮіЪНЮЊy=x+1ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЁпPQЁЭxжсЃЌ
ЁрвдPQЮЊЕзБпЪБЃЌЁїAPQгыЁїBPQЕФУцЛ§жЎБШЕШгкPQБпЩЯЕФИпжЎБШЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЕуDЃЈtЃЌ0ЃЉЃЌAЃЈЉ4ЃЌЉ3ЃЉЃЌBЃЈ3ЃЌ4ЃЉЃЌ
Ёр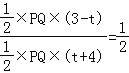 ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЩшжБЯпQMгыЫЋЧњЯпНЛгкCЕуЃЎ
вРЬтвтПЩжЊЃКPЃЈtЃЌ![]() ЃЉЃЌQЃЈtЃЌt+1ЃЉЃЌCЃЈ
ЃЉЃЌQЃЈtЃЌt+1ЃЉЃЌCЃЈ![]() ЃЌt+1ЃЉЃЌ
ЃЌt+1ЃЉЃЌ
ЁрQM=PQ=![]() ЃЌQC=
ЃЌQC=![]() ЃЌ
ЃЌ
ЁрQMЉQC=![]() =
=![]() ЃЌ
ЃЌ
Ёп0ЃМtЃМ3ЃЌ
Ёр0ЃМtЃЈt+1ЃЉЃМ12ЃЌ
Ёр![]() ЃО1ЃЌ
ЃО1ЃЌ
МДQMЉQCЃО0ЃЌ
ЁрQMЃОQCЃЌ
МДБпQMгыЫЋЧњЯп![]() ЪМжегаНЛЕуЃЎ
ЪМжегаНЛЕуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАб 3555ЃЌ4444ЃЌ5333 гЩаЁЕНДѓгУЃМСЌНгЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫуе§ШЗЕФЪЧЃЈ ЃЉ
A.a2+a2=a4
B.ЃЈa2ЃЉ3=a5
C.2aЉa=2
D.ЃЈabЃЉ2=a2b2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЕФМИКЮЬхЕФИЉЪгЭМЪЧ(ЁЁЁЁ)

A. A B. B C. C D. D
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпlОЙ§ЕуA(0ЃЌЃ1)ЃЌЧвгыЫЋЧњЯпyЃН![]() НЛгкЕуB(2ЃЌ1)ЃЎ
НЛгкЕуB(2ЃЌ1)ЃЎ
(1)ЧѓЫЋЧњЯпМАжБЯп lЕФНтЮіЪНЃЛ
(2)вбжЊP(aЃ1ЃЌa)дкЫЋЧњЯпЩЯЃЌЧѓPЕуЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЮЛгкЕквЛЯѓЯоЕФЕуNдкЕквЛЁЂШ§ЯѓЯоЕФНЧЦНЗжЯпЩЯЃЌЧвЕуNЕНyжсЕФОрРыЮЊ2ЃЌдђЕуNЕФзјБъЪЧ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаБфаЮЪєгквЦЯюЕФЪЧ(ЁЁЁЁ)
A. гЩ3xЃНЃ7ЃЋxЃЌЕУ3xЃНxЃ7
B. гЩxЃНyЃЌyЃН0ЃЌЕУxЃН0
C. гЩ7xЃН6xЃ4ЃЌЕУ7xЃЋ6xЃНЃ4
D. гЩ5xЃЋ4yЃН0ЃЌЕУ5xЃНЃ4y
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌНЋШ§НЧАхЗХдке§ЗНаЮABCDЩЯЃЌЪЙШ§НЧАхЕФжБНЧЖЅЕуEгые§ЗНаЮABCDЕФЖЅЕуAжиКЯЃЎШ§НЧАхЕФвЛБпНЛCDгкЕуFЃЌСэвЛБпНЛCBЕФбгГЄЯпгкЕуGЃЎ

ЃЈ1ЃЉЧѓжЄЃКEFЃНEGЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌвЦЖЏШ§НЧАхЃЌЪЙЖЅЕуEЪМжедке§ЗНаЮABCDЕФЖдНЧЯпACЩЯЃЌЦфЫћЬѕМўВЛБфЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌНЋЃЈ2ЃЉжаЕФЁАе§ЗНаЮABCDЁБИФЮЊЁАОиаЮABCDЁБЃЌЧвЪЙШ§НЧАхЕФвЛБпОЙ§ЕуBЃЌЦфЫћЬѕМўВЛБфЃЌШєABЃНaЃЌBCЃНbЃЌЧыжБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com