
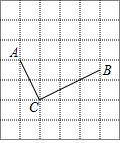
 如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.
如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.分析 (Ⅰ)利用勾股定理计算即可;
(2)设BP=CQ=x,由BC=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$,推出PC=$\frac{3\sqrt{5}}{2}$-x,在Rt△PCQ中,PQ=$\sqrt{{x}^{2}+(\frac{3\sqrt{5}}{2}-x)^{2}}$=$\sqrt{2{x}^{2}-3\sqrt{5}x+\frac{45}{4}}$,对于函数y=2x2-3$\sqrt{5}$x+$\frac{45}{4}$,当x=-$\frac{-3\sqrt{5}}{2×2}$=$\frac{3\sqrt{5}}{4}$时,y有最小值,此时PQ的值最小,此时PC=PB=CQ=$\frac{3}{4}$AC,取BC的中点P,在AC上截取AQ=$\frac{1}{4}$AC,图中PQ即为所求.
解答 解:(Ⅰ)由图象可知AB=$\sqrt{{4}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{65}}{2}$.
(Ⅱ)设BP=CQ=x,
∵BC=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$,
∴PC=$\frac{3\sqrt{5}}{2}$-x,
在Rt△PCQ中,PQ=$\sqrt{{x}^{2}+(\frac{3\sqrt{5}}{2}-x)^{2}}$=$\sqrt{2{x}^{2}-3\sqrt{5}x+\frac{45}{4}}$,
对于函数y=2x2-3$\sqrt{5}$x+$\frac{45}{4}$,当x=-$\frac{-3\sqrt{5}}{2×2}$=$\frac{3\sqrt{5}}{4}$时,y有最小值,此时PQ的值最小,
此时PC=PB=CQ=$\frac{3}{4}$AC.取BC的中点P,在AC上截取AQ=$\frac{1}{4}$AC,图中PQ即为所求.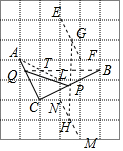
故答案为:取BC的中点P,在AC上截取AQ=$\frac{1}{4}$AC,线段PQ即为所求.
点评 本题考查作图-应用与设计、勾股定理等知识,解题的关键是学会根据二次函数解决最值问题,不同的突破点是求出PQ最小时,CQ的值,属于中考常考题型.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2•3x3=6x3 | B. | 2x2+3x3=5x5 | ||
| C. | -12a3b4÷2a3b2=-6b2 | D. | $\frac{5}{4}$xn•$\frac{2}{5}$xm=$\frac{1}{2}$xmn |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象是一条直线 | B. | 它的图象分布在第一、三象限 | ||
| C. | 点(-1,-5)在它的图象上 | D. | 当x>0时,y随x的增大而增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com