练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．若x2-x-1=0，则5x2-5x+3的值是8．

    分析 直接利用已知得出x2-x=1，再代入原式求出答案．

    解答 解：∵x2-x-1=0，
    ∴x2-x=1，
    ∴5x2-5x+3
    =5（x2-x）+3
    =5+3
    =8．
    故答案为：8．

    点评 此题主要考查了代数式求值，正确应用整体思想是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．如图，小明想测量学校教学楼的高度，教学楼AB的后面有一建筑物CD，他测得当光线与地面成22°的夹角时，教学楼在建筑物的墙上留下高2m高的影子CE；而当光线与地面成45°的夹角时，教学楼顶A在地面上的影子F与墙角C有13m的距离（点B，F，C在同一条直线上）
    （1）请你帮小明计算一下学校教学楼的高度；
    （2）为了迎接上级领导检查，学校准备在AE之间挂一些彩旗，请计算AE之间的长．（结果精确到1m，参考数据：sin22°≈0.375，cos22°≈0.9375，tan22°≈0.4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

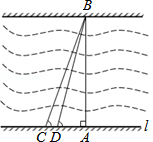    10．黄冈市为了改善市区交通状况，计划修建一座新大桥．如图，新大桥的两端位于A、B两点，小张为了测量A、B之间的河宽，在垂直于新大桥AB的直线型道路l上测得如下数据：∠BDA=76.1°，∠BCA=68.2°，CD=82米．求AB的长（精确到0.1米）．
    参考数据：sin76.1°≈0.97，cos76.1°≈0.24，tan76.1°≈4.0；sin68.2°≈0.93，cos68.2°≈0.37，tan68.2°≈2.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列方程中一定是一元二次方程的是（　　）
    A．x2-6x=x2+9B．（x-1）（x+2）=0C．ax2-6x=0D．（a-3）x2=5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知方程（$\frac{2}{x}$+1）2-$\frac{2x+4}{x}$-3=0，如果设$\frac{2}{x}$+1=y，那么原方程化为关于y的方程是y2-2y-3=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．在方程$\left\{\begin{array}{l}{x=2}\\{3y-x=1}\end{array}\right.$、$\left\{\begin{array}{l}{x+y=0}\\{3x-y=5}\end{array}\right.$、$\left\{\begin{array}{l}{xy=1}\\{x+2y=3}\end{array}\right.$、$\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=1}\\{x+y=1}\end{array}\right.$、$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$中，是二元一次方程组的有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图（1），点A是反比例函数y=$\frac{4}{x}$的图象在第一象限内一动点，过A作AC⊥x轴于点C，连接OA并延长到点B，过点B作BD⊥x 轴于点D，交双曲线于点E，连结OE．
    （1）若S△OBE=6，求经过点B的反比例函数解析式．
    （2）如图（2），过点B作BF⊥y 轴于点F，交双曲线于点G．
    ①延长OA到点B，当AB=OA时，请判断FG与BG之间的数量关系，并说明理由．
    ②当AB=nOA时，请直接写出FG与BG之间的数量关系．

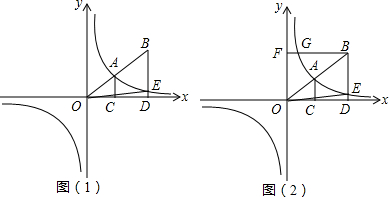
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若一个圆锥底面圆的半径为3cm，高为4cm，则这个圆锥的侧面积为15πcm2．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．把多项式16m3-mn2分解因式的结果是m（4m+n）（4m-n）．

    查看答案和解析>>

    同步练习册答案