
”¾ĢāÄæ”抔Ć÷ŗĶ¼øĪ»Ķ¬Ń§×öŹÖµÄÓ°×ÓÓĪĻ·Ź±£¬·¢ĻÖ¶ŌÓŚĶ¬Ņ»ĪļĢ壬Ӱ×ӵēóŠ”Óė¹āŌ“µ½ĪļĢåµÄ¾ąĄėÓŠ¹Ų.Ņņ“Ė£¬ĖūĆĒČĻĪŖ£ŗæÉŅŌ½čÖśĪļĢåµÄÓ°×Ó³¤¶Č¼ĘĖć¹āŌ“µ½ĪļĢåµÄĪ»ÖĆ.ÓŚŹĒ£¬ĖūĆĒ×öĮĖŅŌĻĀ³¢ŹŌ.
£Ø1£©ČēĶ¼¢Ł£¬“¹Ö±ÓŚµŲĆę·ÅÖƵÄÕż·½ŠĪæņ¼ÜABCD£¬±ß³¤ABĪŖ30cm£¬ŌŚĘäÕżÉĻ·½ÓŠŅ»µĘÅŻ£¬ŌŚµĘÅŻµÄÕÕÉäĻĀ£¬Õż·½ŠĪæņ¼ÜµÄŗįĻņÓ°×ÓA”äB£¬D”äCµÄ³¤¶ČŗĶĪŖ6cm.ÄĒĆ“µĘÅŻĄėµŲĆęµÄø߶ČĪŖ .
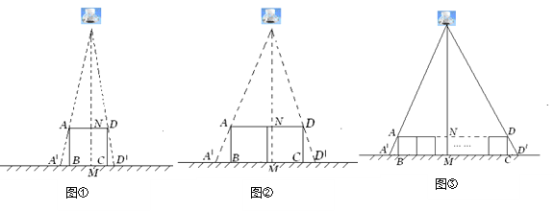 £Ø2£©²»øÄ±ä¢ŁÖŠµĘÅŻµÄøß¶Č£¬½«Į½øö±ß³¤ĪŖ30cmµÄÕż·½ŠĪæņ¼Ü°“Ķ¼¢Ś°Ś·Å£¬Ēė¼ĘĖć“ĖŹ±ŗįĻņÓ°×ÓA”äB£¬D”äCµÄ³¤¶ČŗĶĪŖ¶ąÉŁ£æ
£Ø2£©²»øÄ±ä¢ŁÖŠµĘÅŻµÄøß¶Č£¬½«Į½øö±ß³¤ĪŖ30cmµÄÕż·½ŠĪæņ¼Ü°“Ķ¼¢Ś°Ś·Å£¬Ēė¼ĘĖć“ĖŹ±ŗįĻņÓ°×ÓA”äB£¬D”äCµÄ³¤¶ČŗĶĪŖ¶ąÉŁ£æ
£Ø3£©ÓŠnøö±ß³¤ĪŖaµÄÕż·½ŠĪ°“Ķ¼¢Ū°Ś·Å£¬²āµĆŗįĻņÓ°×ÓA”äB£¬D”äCµÄ³¤¶ČŗĶĪŖb,ĒóµĘÅŻĄėµŲĆęµÄ¾ąĄė.£ØŠ“³ö½āĢā¹ż³Ģ£¬½į¹ūÓĆŗ¬a,b,nµÄ“śŹżŹ½±ķŹ¾£©
”¾“š°ø”æ£Ø1£©180cm £Ø2£©12 cm (3) ![]()
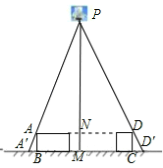
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÉčµĘÅŻµÄĪ»ÖĆĪŖµćP£¬Ņ׵Ɣ÷PAD”×”÷PA”äD”䣬Éč³öĖłĒóµÄĪ“ÖŖŹż£¬ĄūÓĆĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ßµÄ±ČµČÓŚ¶ŌÓ¦øßµÄ±Č£¬æɵƵĘÅŻĄėµŲĆęµÄøß¶Č£»
£Ø2£©Ķ¬·ØæɵƵ½ŗįĻņÓ°×ÓA”äB£¬D”äCµÄ³¤¶ČŗĶ£»
£Ø3£©°“ÕÕĻąÓ¦µÄČż½ĒŠĪĻąĖĘ£¬ĄūÓĆĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ßµÄ±ČµČÓŚ¶ŌÓ¦øßµÄ±Č£¬ÓĆ×ÖÄø±ķŹ¾³öĘäĖūĻ߶Ī£¬¼“æɵƵ½µĘÅŻĄėµŲĆęµÄ¾ąĄė£®
½ā£ŗ£Ø1£©ÉčµĘÅŻĄėµŲĆęµÄø߶ČĪŖxcm£¬
”ßAD”ĪA”äD”䣬
”ą”ĻPAD=”ĻPA”äD”䣬”ĻPDA=”ĻPD”äA”䣮
”ą”÷PAD”×”÷PA”äD”䣮
øł¾ŻĻąĖĘČż½ĒŠĪ¶ŌÓ¦øߵıȵČÓŚĻąĖʱȵĊŌÖŹ£¬æɵĆ![]() £¬
£¬
”ą![]() =
=![]() £¬
£¬
½āµĆx=180£®£Ø4·Ö£©
£Ø2£©ÉčŗįĻņÓ°×ÓA”äB£¬D”äCµÄ³¤¶ČŗĶĪŖycm£¬
Ķ¬ĄķæɵƔą![]() =
=![]() £¬
£¬
½āµĆy=12cm£»£Ø3·Ö£©
£Ø3£©¼ĒµĘÅŻĪŖµćP£¬ČēĶ¼£ŗ
”ßAD”ĪA”äD”䣬”ą”ĻPAD=”ĻPA”äD”䣬”ĻPDA=”ĻPD”äA”䣮
”ą”÷PAD”×”÷PA”äD”䣮
øł¾ŻĻąĖĘČż½ĒŠĪ¶ŌÓ¦øߵıȵČÓŚĻąĖʱȵĊŌÖŹ£¬æɵĆ![]() £Ø1·Ö£©
£Ø1·Ö£©
£ØÖ±½ÓµĆ³öČż½ĒŠĪĻąĖĘ»ņ±ČĄżĻ߶Ī¾ł²»æŪ·Ö£©
ÉčµĘÅŻĄėµŲĆę¾ąĄėĪŖx£¬ÓÉĢāŅā£¬µĆPM=x£¬PN=x©a£¬AD=na£¬A”äD”ä=na+b£¬
”ą![]() =1©
=1©![]()
![]() =1©
=1©![]()
x=![]() £Ø1·Ö£©£®
£Ø1·Ö£©£®


 Ź±æĢ×¼±ø×ÅŹī¼Ł×÷ŅµŌ×ÓÄܳö°ęÉēĻµĮŠ“š°ø
Ź±æĢ×¼±ø×ÅŹī¼Ł×÷ŅµŌ×ÓÄܳö°ęÉēĻµĮŠ“š°ø Źī¼ŁĻĪ½Ó½Ģ²ÄĘŚÄ©Źī¼ŁŌ¤Ļ°Īäŗŗ³ö°ęÉēĻµĮŠ“š°ø
Źī¼ŁĻĪ½Ó½Ģ²ÄĘŚÄ©Źī¼ŁŌ¤Ļ°Īäŗŗ³ö°ęÉēĻµĮŠ“š°ø ¼ŁĘŚ×÷ŅµŹī¼Ł³É³¤ĄÖŌ°ŠĀ½®ĒąÉŁÄź³ö°ęÉēĻµĮŠ“š°ø
¼ŁĘŚ×÷ŅµŹī¼Ł³É³¤ĄÖŌ°ŠĀ½®ĒąÉŁÄź³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
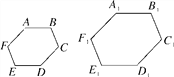
”¾ĢāÄæ”æĶ¼ÖŠµÄĮ½øö¶ą±ßŠĪABCDEFŗĶA1B1C1D1E1F1ĻąĖĘ(ø÷×ÖÄøŅŃ°“¶ŌÓ¦¹ŲĻµÅÅĮŠ)£¬”ĻA£½”ĻD1£½135”ć£¬”ĻB£½”ĻE1£½120”ć£¬”ĻC1£½95”ć.
(1)Ēó”ĻFµÄ¶ČŹż£»
(2)Čē¹ū¶ą±ßŠĪABCDEFŗĶA1B1C1D1E1F1µÄĻąĖʱȏĒ1£ŗ1.5£¬ĒŅCD£½15cm£¬ĒóC1D1µÄ³¤¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
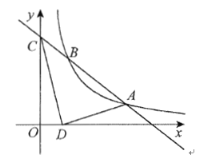
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹż![]() µÄĶ¼ĻńÓė·“±ČĄżŗÆŹż
µÄĶ¼ĻńÓė·“±ČĄżŗÆŹż![]() µÄĶ¼Ļń½»ÓŚµć
µÄĶ¼Ļń½»ÓŚµć![]() ŗĶµć
ŗĶµć![]() £¬Óė
£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() .
.
(1)·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½ £»Ņ»“ĪŗÆŹżµÄ±ķ“ļŹ½ .
(2)ČōŌŚ![]() ÖįÉĻÓŠŅ»µć
ÖįÉĻÓŠŅ»µć![]() £¬Ęäŗį×ų±źŹĒ1£¬Į¬½Ó
£¬Ęäŗį×ų±źŹĒ1£¬Į¬½Ó![]() £¬Ēó
£¬Ēó![]() µÄĆ껿.
µÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖACŹĒĮāŠĪABCDµÄ¶Ō½ĒĻߣ¬”ĻBAC£½60”ć£¬µćEŹĒÖ±ĻßBCÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓAE£¬ŅŌAEĪŖ±ß×÷ĮāŠĪAEFG£¬²¢ĒŅŹ¹”ĻEAG£½60”ć£¬Į¬½ÓCG£¬µ±µćEŌŚĻ߶ĪBCÉĻŹ±£¬ČēĶ¼1£¬Ņ×Ö¤£ŗAB£½CG£«CE.
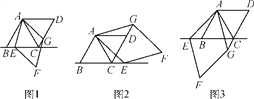
(1)µ±µćEŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻŹ±(ČēĶ¼2)£¬²ĀĻėAB£¬CG£¬CEÖ®¼äµÄ¹ŲĻµ²¢Ö¤Ć÷£»
(2)µ±µćEŌŚĻ߶ĪCBµÄŃÓ³¤ĻßÉĻŹ±(ČēĶ¼3)£¬Ö±½ÓŠ“³öAB£¬CG£¬CEÖ®¼äµÄ¹ŲĻµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
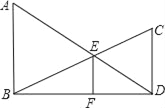
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬AB”ĶBD£¬CD”ĶBD£¬“¹×ć·Ö±šĪŖB”¢D£¬ADŗĶBCĻą½»ÓŚµćE£¬EF”ĶBD£¬“¹×ćĪŖF£¬ĪŅĆĒæÉŅŌÖ¤Ć÷![]() ³ÉĮ¢£Ø²»ŅŖĒóæ¼ÉśÖ¤Ć÷£©£®
³ÉĮ¢£Ø²»ŅŖĒóæ¼ÉśÖ¤Ć÷£©£®
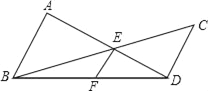
Čō½«Ķ¼ÖŠµÄ“¹ĻßøÄĪŖŠ±½»£¬ČēĶ¼£¬AB”ĪCD£¬AD£¬BCĻą½»ÓŚµćE£¬¹żµćE×÷EF”ĪAB½»BDÓŚµćF£¬Ōņ£ŗ
£Ø1£©![]() »¹³ÉĮ¢Āš£æČē¹ū³ÉĮ¢£¬Ēėøų³öÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
»¹³ÉĮ¢Āš£æČē¹ū³ÉĮ¢£¬Ēėøų³öÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø2£©ĒėÕŅ³öS”÷ABD£¬S”÷BEDŗĶS”÷BDC¼äµÄ¹ŲĻµŹ½£¬²¢øų³öÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×ŅŅĮ½ČĖ×öÖĄŅ»øö¾łŌČŠ”Į¢·½ĢåµÄÓĪĻ·£¬Į¢·½ĢåµÄĆæøöĆęÉĻ·Ö±š±źÓŠŹż×Ö1£¬2£¬3£¬4£¬5£¬6£¬ČĪŅāÖĄ³öŠ”Į¢·½Ģåŗó£¬Čō³ÆÉĻµÄŹż×ÖŠ”ÓŚ3£¬Ōņ¼×»ńŹ¤£»Čō³ÆÉĻµÄŹż×Ö“óÓŚ3 £¬ŌņŅŅ»ńŹ¤£®ÄćČĻĪŖÕāøöÓĪĻ·¶Ō¼×ŅŅĖ«·½¹«Ę½Āš£æĪŖŹ²Ć“£æÄćÄܲ»ÄܾĶÉĻĆęµÄŠ”Į¢·½ĢåÉč¼ĘŅ»øö½ĻĪŖ¹«Ę½µÄÓĪĻ·£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£Ø1£©£¬![]() µÄ¶„µć
µÄ¶„µć![]() ”¢
Ӣ![]() Ӣ
”¢![]() ·Ö±šÓėÕż·½ŠĪ
·Ö±šÓėÕż·½ŠĪ![]() µÄ¶„µć
µÄ¶„µć![]() ”¢
Ӣ![]() Ӣ
”¢![]() ÖŲŗĻ.
ÖŲŗĻ.
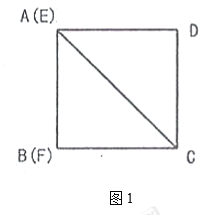
£Ø1£©ČōÕż·½ŠĪµÄ±ß³¤ĪŖ![]() £¬ÓĆŗ¬
£¬ÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾£ŗÕż·½ŠĪ
µÄ“śŹżŹ½±ķŹ¾£ŗÕż·½ŠĪ![]() µÄÖܳ¤µČÓŚ_______£¬
µÄÖܳ¤µČÓŚ_______£¬![]() µÄĆ껿µČÓŚ_______.
µÄĆ껿µČÓŚ_______.
£Ø2£©ČēĶ¼2£¬½«![]() Čʵć
Čʵć![]() Ė³Ź±ÕėŠż×Ŗ£¬±ß
Ė³Ź±ÕėŠż×Ŗ£¬±ß![]() ŗĶÕż·½ŠĪµÄ±ß
ŗĶÕż·½ŠĪµÄ±ß![]() ½»ÓŚµć
½»ÓŚµć![]() .Į¬½į
.Į¬½į![]() £¬É芿×Ŗ½Ē
£¬É芿×Ŗ½Ē![]() .
.

¢ŁŹŌĖµĆ÷![]() £»
£»
¢ŚČō![]() ÓŠŅ»øöÄŚ½ĒµČÓŚ
ÓŠŅ»øöÄŚ½ĒµČÓŚ![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
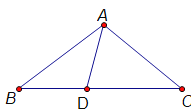
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼¦¤ABCÖŠ£¬AB£½AC£¬DµćŌŚBCÉĻ£¬ĒŅBD£½AD£¬DC£½AC£®²¢Ēó”ĻBµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø6·Ö£©ČēĶ¼¢ŁĖłŹ¾£¬½«Ö±³ß°Ś·ÅŌŚČż½Ē°åABCÉĻ£¬Ź¹Ö±³ßÓėČż½Ē°åµÄ±ß·Ö±š½»ÓŚµćD£¬E£¬F£¬G£¬ĮæµĆ”ĻCGD=42”ć”£

£Ø1£©Ēó”ĻCEFµÄ¶ČŹż£»
£Ø2£©½«Ö±³ßĻņĻĀĘ½ŅĘ£¬Ź¹Ö±³ßµÄ±ßŌµĶعżČż½Ē°åµÄ¶„µćB£¬½»AC±ßÓŚµćH£¬ČēĶ¼¢ŚĖłŹ¾£®µćH£¬BŌŚÖ±³ßÉĻµÄ¶ĮŹż·Ö±šĪŖ4£¬13£®4£¬ĒóBCµÄ³¤£Ø½į¹ū±£ĮōĮ½Ī»Š”Źż£©£®
£Ø²Īæ¼Źż¾Ż£ŗsin42”ć”Ö0£®67£¬cos42”ć”Ö0£®74£¬tan42”ć”Ö0£®90£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com