练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．我们称使$\frac{a}{2}$+$\frac{b}{3}$=$\frac{a+b}{2+3}$成立的一对数a，b为“相伴数对”，记为（a，b），如：当a=b=0时，等式成立，记为（0，0）．若（a，3）是“相伴数对”，则a的值为-$\frac{4}{3}$．

    分析 根据“相伴数对”的定义，即可得出关于a的一元一次方程，解之即可得出结论．

    解答 解：∵（a，3）是“相伴数对”，
    ∴$\frac{a}{2}$+$\frac{3}{3}$=$\frac{a+3}{2+3}$，
    解得：a=-$\frac{4}{3}$．
    故答案为：-$\frac{4}{3}$．

    点评 本题考查了解一元一次方程，依照“相伴数对”的定义找出关于a的一元一次方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

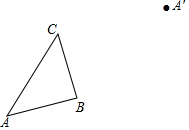    10．用直尺和圆规作图：已知△ABC与△A′B′C′成中心对称（点A与A′对应），请在图中画出对称中心O，并画出完整的△A′B′C′．（保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．据媒体报道，我国因环境污染造成的巨大经济损失，每年高达860 000 000元，这个数用科学记数法表示为8.6×108元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．我国年可利用的淡水资源总量为27500亿米3，27500亿这个数用科学记数法表示为2.75×1012．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

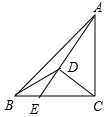    3．如图，在△ABC中，∠ACB=90°，D在△ABC内，DB=DC，连接AD并延长交BC于F，且AD=BC，若DE=3，BE=5，则CE的长为8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．x2+（p+q）x+pq型式子的因式分解
    ∵x2+（p+q）x+pq=x2+px+qx+pq
    =（x2+px）+（qx+pq）（加法结合律）
    =x（x+p）+q（x+p）
    =（x+p）（x+q）
    ∴我们得到x2+（p+q）x+pq=（x+p）（x+q）①
    利用①式可以将某些二次项系数为1的二次三项式分解因式．
    例把x2+3x+2分解因式
    分析：x2+3x+2中的二次项系数为1，常数项2=1×2，一次项系数3=1+2，这是一个x2+（p+q）x+pq型式子．
    ∴解：x2+3x+2=（x+1）（x+2）
    请仿照上面的方法将下列多项式分解因式：
    ①x2+7x+10=（x+2）（x+5）；　　　②x2-2y-8=（y-4）（y+2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．绿色无公害蔬菜基地有甲、乙两种植户，他们种植了A，B两类蔬菜，两种植户种植的两类蔬菜的种植面积与总收入如下表：
    种植户种植A类蔬菜面积
    （单位：亩）    		种植B类蔬菜面积
    （单位：亩）    		总收入
    （单位：元）
    甲3112500
    乙2316500
    说明：不同种植户种植的同类蔬菜每亩的平均收入相等；亩为土地面积单位．
    （1）求A、B两类蔬菜每亩的平均收入各是多少元；
    （2）某种植户准备租20亩地用来种植A、B两类蔬菜，为了使总收入不低于63000元，且种植A类蔬菜的面积多于种植B类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租地方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图所示，图中∠1与∠2是同位角的是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列函数中，是反比例函数的为（　　）
    A．y=2x+1B．y=$\frac{2}{{x}^{2}}$C．y=$\frac{3}{x}$D．2y=x

    查看答案和解析>>

    同步练习册答案