
【题目】在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中点为点M,则线段AM的长为 .
【答案】5.5,或0.5
【解析】解:分两种情况:①如图1所示: 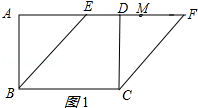
∵四边形ABCD是矩形,
∴CD=AB=4,BC=AD=5,∠ADC=∠CDF=90°,
∵四边形BCFE为菱形,
∴CF=EF=BE=BC=5,
∴DF= ![]() =
= ![]() =3,
=3,
∴AF=AD+DF=8,
∵M是EF的中点,
∴MF= ![]() EF=2.5,
EF=2.5,
∴AM=AF﹣DF=8﹣2.5=5.5;
②如图2所示:同①得:AE=3,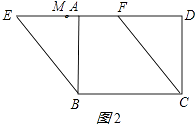
∵M是EF的中点,
∴ME=2.5,
∴AM=AE﹣ME=0.5;
综上所述:线段AM的长为:5.5,或0.5;
故答案为:5.5,或0.5.
两种情况:①由矩形的性质得出CD=AB=4,BC=AD=5,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=5,由勾股定理求出DF,得出MF,即可求出AM;②同①得出AE=3,求出ME,即可得出AM的长.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,求证:∠3=∠B
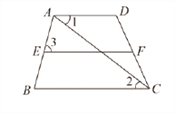
证明:
∵∠D=110°,∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥EF( )
又∵∠1=∠2(已知)
∴ ∥ (内错角相等,两直线平行)
∴EF∥BC( )
∴∠3=∠B( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点P′(x0+5,y0-2).
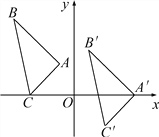
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )

A.24 B.12 C.6 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2). 
回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数、中位数;
(3)请你计算平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com