
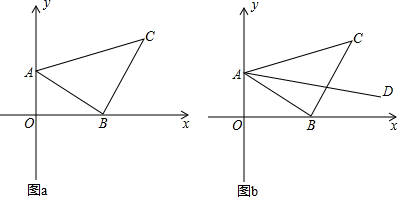
分析 (1)先根据△ABC是等腰直角三角形,以及∠CAO=105°,求得∠BAO=60°,再根据∠ABO=30°,以及A(0,2),求得△ABC的面积即可;
(2)先过C作CE⊥x轴于E,构造全等三角形,根据全等三角形的对应边相等,即可得出BE=AO=2,CE=BO=m,OE=2+m,据此得出C的坐标为(2+m,m);
(3)先作点N关于AD的对称点N',连接MN,MN',根据轴对称的性质得出MN=MN',再根据当点C、M、N'在同一直线上,且CN'⊥AB时,CN'最短,得出点N'与点B重合,点M为BC与AD的交点,最后根据OB=3,AO=2,在Rt△AOB中,求得AB=$\sqrt{13}$=CB,即可得出CM+MN的最小值为$\sqrt{13}$.
解答 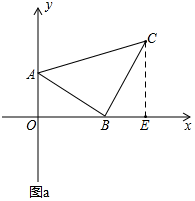 解:(1)如图a,∵BC⊥AB,BC=AB,
解:(1)如图a,∵BC⊥AB,BC=AB,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∵∠CAO=105°,
∴∠BAO=105°-45°=60°,
∵∠AOB=90°,
∴∠ABO=30°,
∵A(0,2),
∴AO=2,AB=4,
∴由勾股定理可得OB=2$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×AO×BO=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$;
(2)如图a,过C作CE⊥x轴于E,则∠CEB=∠BOA=90°,∠BCE+∠CBE=90°,
∵AB⊥BC,
∴∠ABO+∠CBE=90°,
∴∠BCE=∠ABO,
在△BCE和△ABO中,
$\left\{\begin{array}{l}{∠BCE=∠ABO}\\{∠CEB=∠BOA}\\{BC=AB}\end{array}\right.$,
∴△BCE≌△ABO(AAS),
又∵点A(0,2),点B(m,0),
∴BE=AO=2,CE=BO=m,
∴OE=2+m,
∴C的坐标为(2+m,m);
(3)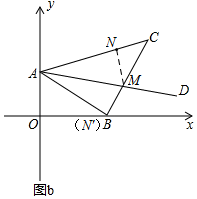 ∵M在射线AD上,N在边AC上,AD是∠CAB的平分线,
∵M在射线AD上,N在边AC上,AD是∠CAB的平分线,
∴点N关于AD的对称点在AB上,
如图b,作点N关于AD的对称点N',连接MN,MN',则MN=MN',
∴CM+MB=CM+MN',
当点C、M、N'在同一直线上,且CN'⊥AB时,CN'最短,
∵CB⊥AB,
∴此时,点N'与点B重合,点M为BC与AD的交点,
当m=3时,OB=3,AO=2,
∴Rt△AOB中,AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴CB=$\sqrt{13}$,即CN'=$\sqrt{13}$,
∴CM+MN的最小值为$\sqrt{13}$.
点评 本题属于三角形综合题,主要考查了轴对称的性质,垂线段最短,等腰直角三角形的性质以及全等三角形的判定与性质的综合应用,根据垂线段最短,确定出点M、N的位置是解题的关键.最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:填空题
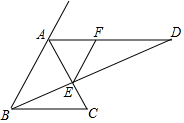 如图:在△ABC中,AB=AC,BE平分∠ABC,AD∥BC,AD交BE的延长线于D,EF平分∠AED,若AB=8,AF=3,AE:ED=AF:FD,则CE=$\frac{7}{2}$.
如图:在△ABC中,AB=AC,BE平分∠ABC,AD∥BC,AD交BE的延长线于D,EF平分∠AED,若AB=8,AF=3,AE:ED=AF:FD,则CE=$\frac{7}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
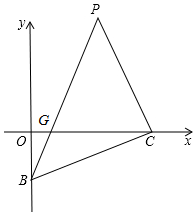 如图,点D(m,n)满足m2-6m+$\sqrt{m+n-6}$=-9,B为y轴负半轴上一动点,∠DBC=45°,BC交x轴于C,CP⊥BC交BD延长线于P,交x轴于点G.
如图,点D(m,n)满足m2-6m+$\sqrt{m+n-6}$=-9,B为y轴负半轴上一动点,∠DBC=45°,BC交x轴于C,CP⊥BC交BD延长线于P,交x轴于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
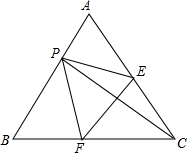 如图,等边三角形ABC的边长为1,P是AB边上的一个动点(P与A,B不重合),将其折叠点C与点P重合,折痕为EF.
如图,等边三角形ABC的边长为1,P是AB边上的一个动点(P与A,B不重合),将其折叠点C与点P重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在方格纸中,点A,C,D,E,F都在格点上,且直线AC与CD互相垂直.
如图,在方格纸中,点A,C,D,E,F都在格点上,且直线AC与CD互相垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com