练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若y+2与x-3成正比例，当x=0时，y=1；则当x=1时，y的值是


    1. A.
      -1
    2. B.
      0
    3. C.
      1
    4. D.
      2
    B
    分析：若y+2与x-3成正比例，即可表示为y+2=k（x-3），把x=0，y=1代入即可求得k的值，进而把x=1代入解析式求得y的值．
    解答：设y+2=k（x-3），把x=0，y=1代入
    得：3=k（0-3）
    解得：k=-1
    则解析式是：y+2=-1（x-3）
    把x=1代入，解得y=0．
    故选B．
    点评：此类题目需灵活运用待定系数法建立函数解析式，然后将点的坐标代入解析式，利用方程解决问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    5、横坐标、纵坐标都是整数的点是整点坐标．若直线y=-2x+k（k为正整数），与坐标轴围成三角形内的整点坐标（含周界）的个数是100，则k等于（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，正三角形、正方形、正六边形等正n边形与圆的形状有差异，我们将正n边形与圆的接近程度称为“接近度”、在研究“接近度”时，应保证相似图形的“接近度”相等、
    （1）设正n边形的每个内角的度数为m°，将正n边形的“接近度”定义为|180-m|、于是，|180-m|越小，该正n边形就越接近于圆，
    ①若n=20，则该正n边形的“接近度”等于
     
    ；
    ②当“接近度”等于
     
    时，正n边形就成了圆．
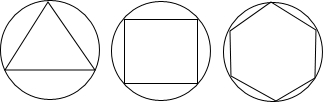    （2）设一个正n边形的半径（即正n边形外接圆的半径）为R，边心距（即正n边形的中心到各边的距离）为r，将正n边形的“接近度”定义为|R-r|，于是|R-r|越小，正n边形就越接近于圆；你认为这种说精英家教网法是否合理？若不合理，请给出正n边形“接近度”的一个合理定义．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知一次函数y=kx+b的图象为直线l，直线l过点P（2，1）且与x，y轴的正半轴分别交于A，B两点，若直线l与x、y轴围成的三角形的面积为5，则这样的直线l共有（　　）
    A、1条B、2条C、3条D、4条

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （2013•镇江）【阅读】
    如图1，在平面直角坐标系xOy中，已知点A（a，0）（a＞0），B（2，3），C（0，3）．过原点O作直线l，使它经过第一、三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．
    【理解】
    若点D与点A重合，则这个操作过程为FZ[
    45°
    45°
    ，
    3
    3
    ]；
    【尝试】
    （1）若点D恰为AB的中点（如图2），求θ；
    （2）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形0ABC的边AB上，求出a的值；若点E落在四边形0ABC的外部，直接写出a的取值范围；
    【探究】
    经过FZ[θ，a]操作后，作直线CD交x轴于点G，交直线AB于点H，使得△ODG与△GAH是一对相似的等腰三角形，直接写出FZ[θ，a]．

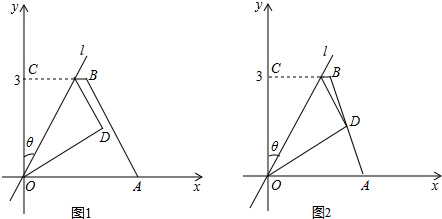
    查看答案和解析>>

    科目：初中数学 来源： 题型：

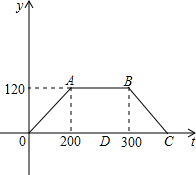    小明参加汽车驾驶培训，在实际操作考试时，被要求进行启动加速、匀速运行、制动减速三个连贯过程，在加速和减速运动过程中，路程和速度均满足关系s=v0t+
    12
    at2    ，v0为加速或减速的起始速度，加速时a为正，减速时a为负，匀速时a=0，加速或减速t秒后的瞬时速度v=v0+at，小明在操作中瞬时速度v与时间t的关系如图所示，其中OA为匀加速，AB为匀速，BC为匀减速．
    （1）若减速过程与加速过程完全相反，即BC与OA关于AB的中垂线成轴对称，求BC的解析式．
    （2）当0≤t≤300时，求汽车行驶的路程s与时间t的函数关系式．
    （3）汽车行驶t秒后，
    ①若经途中D点，过点D作垂线交AB于点E，试证明汽车行驶的路程恰等于四边形OAED的面积．
    ②若汽车行驶至M点，过点M做垂线交BC于点N，汽车行驶的路程是否等于五边形OABNM的面积呢？试说明理由．

    查看答案和解析>>

    同步练习册答案