
【题目】在乌海棚户区改造中,有一部分楼盘要对外销售. 某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,从第八层起每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2. 若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:只降价10%,没有其他赠送.
(1)求出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)直接填写答案:老王要购买第十六层的一套楼房,他一次性付清购房款,用方案一,这套楼房总费用为__________元;当a=__________时两种优惠方案总费用相同;
当a<__________时,用方案二合算.
【答案】(1) ![]() ;(2)485760-a ;10560; 10560.
;(2)485760-a ;10560; 10560.
【解析】分析:(1)根据题意分别求出当1≤x≤8时,每平方米的售价应为4000-(8-x)×30元,当9≤x≤23时,每平方米的售价应为4000+(x-8)×50元;(2)根据购买方案一、二求出实交房款的关系式,然后分情况讨论即可确定那种方案合算.
本题解析:(1)当1≤x≤8时,y=4000-30(8-x)
=4000-240+30 x
=30 x+3760;
当8<x≤23时,y=4000+50(x-8)
=4000+50 x-400
=50 x+3600.
∴所求函数关系式为![]()
(2)当x=16时,用方案一的每套楼房总费用为:
w1=120(50×16+3600)×92%-a=485760-a;
方案二每套楼房总费用:
w2=120(50×16+3600)×90%=475200
∴当w1=w2时,即485760-a=475200时,a=10560;
因此,当每套赠送装修基金a=10560元时两种方案总费用一样;
当每套赠送装修基金a <10560元时,用方案二合算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】A,B 两地相距 200 千米,甲车以每小时 48 千米的速度从 A 地驶向 B 地,乙车以每小时 32 千米的速度从 B地驶向 A 地,若两车同时出发,________小时后两车相距 40 千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程:
计算:(-15)÷(![]() -1
-1![]() -3)×6.
-3)×6.
解:原式=(-15)÷(-![]() )×6(第一步)
)×6(第一步)
=(-15)÷(-25)(第二步)
=![]() .(第三步)
.(第三步)
解答:(1)上面解题过程,从第____步开始错误,错误的原因是_____.
(2)请写出正确的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
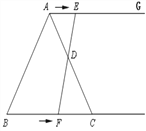
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s) ;
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)求当t为何值时,四边形ACFE是菱形;
(3)是否存在某一时刻t,使以A、F、C、E为顶点的四边形内角出现直角?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙、丙三位同学分别设计出如下几种方案:
甲:如图①,先在平地取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的长即为A,B的距离.
乙:如图②,先过点B作AB的垂线,再在垂线上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为A,B的距离.
丙:如图③,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA,这时只要测出BC的长即为A,B的距离.
(1)以上三位同学所设计的方案,可行的有_______________;
(2)请你选择一可行的方案,说说它可行的理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com