
 ШчЭМЃЌвбжЊЖўДЮКЏЪ§y=ax2+bx+4ЕФЭМЯѓгыyжсНЛгкЕуAЃЌгыxжсНЛгкBЃЈ-2ЃЌ0ЃЉЁЂCЃЈ8ЃЌ0ЃЉСНЕуЃЌЦфЖдГЦжсгыxжсНЛгкЕуDЃЌСЌНгACЁЂABЃЎ
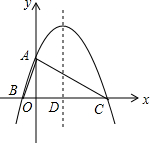
ШчЭМЃЌвбжЊЖўДЮКЏЪ§y=ax2+bx+4ЕФЭМЯѓгыyжсНЛгкЕуAЃЌгыxжсНЛгкBЃЈ-2ЃЌ0ЃЉЁЂCЃЈ8ЃЌ0ЃЉСНЕуЃЌЦфЖдГЦжсгыxжсНЛгкЕуDЃЌСЌНгACЁЂABЃЎЗжЮі ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИљОнНтЮіЪНЧѓЕУAЕФзјБъЃЌИљОнЙДЙЩЖЈРэЧѓЕУABЁЂACЁЂBCЕФГЄЃЌдйИљОнЙДЙЩЖЈРэЕФФцЖЈРэМДПЩХаЖЈЁїABCЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉЗжРрЬжТлЃКЕБCD=DEЪБЃЌЕБEC=DEЪБЃЌЕБCD=CEЪБЃЌИљОнЕШбќШ§НЧаЮЕФЖЈвхЃЌПЩЕУЙигкmЕФЗНГЬЃЌИљОнНтЗНГЬЃЌПЩЕУД№АИЃЎ
ЃЈ4ЃЉЗжШ§жжЧщПіЬжТлМДПЩЧѓЕУЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпЖўДЮКЏЪ§y=ax2+bx+4ЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкBЃЈ-2ЃЌ0ЃЉЁЂCЃЈ8ЃЌ0ЃЉСНЕуЃЌ
Ёр$\left\{\begin{array}{l}{4a-2b+4=0}\\{64a+8b+4=0}\end{array}\right.$
НтЕУ$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\end{array}\right.$ЃЌ
ЁрИУЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4ЃЛ
ЃЈ2ЃЉСюx=0ЃЌдђy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=4ЃЌ
ЁрAЃЈ0ЃЌ4ЃЉЃЌ
ЁпBЃЈ-2ЃЌ0ЃЉЁЂCЃЈ8ЃЌ0ЃЉЃЌ
ЁрAB2=42+22=20ЃЌAC2=82+42=80ЃЌBC2=ЃЈ8+2ЃЉ2=100ЃЌ
ЁрAB2+AC2=BC2ЃЌ
ЁрЁїABCЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉдкЯпЖЮBCЩЯЪЧДцдкЕуEЃЌЪЙЕУЁїCDEЮЊЕШбќШ§НЧаЮЃЌ
гЩЖўДЮКЏЪ§y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4жЊЖдГЦжсx=3ЃЌ
ЁрDЃЈ3ЃЌ0ЃЉЃЎ
ЁпCЃЈ8ЃЌ0ЃЉЃЌ
ЁрCD=5ЃЎ
ЩшACЕФНтЮіЪНЮЊy=kx+bЃЌ
НЋAЁЂCЕузјБъДњШыЃЌЕУ$\left\{\begin{array}{l}{8k+b=0}\\{b=4}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$ЃЌ
ACЕФНтЮіЪНЮЊy=-$\frac{1}{2}$x+4ЃЎ
EдкЯпЖЮACЩЯЃЌЩшEЕузјБъЮЊЃЈmЃЌ-$\frac{1}{2}$m+4ЃЉЃЎ
ЂйЕБCD=DEЪБЃЌМДЃЈm-3ЃЉ2+ЃЈ-$\frac{1}{2}$m+4ЃЉ2=25ЃЌНтЕУm1=0ЃЌm2=8ЃЈВЛЗћКЯЬтвтЩсШЅЃЉЃЌ
ЕБm=0ЪБЃЌ-$\frac{1}{2}$m+4=4ЃЌ
ЁрE1ЃЈ0ЃЌ4ЃЉЃЛ
ЂкЕБEC=DEЪБЃЌЃЈm-8ЃЉ2+ЃЈ-$\frac{1}{2}$m+4ЃЉ2=ЃЈm-3ЃЉ2+ЃЈ-$\frac{1}{2}$m+4ЃЉ2ЃЌНтЕУm3=$\frac{11}{2}$ЃЌ
ЕБm=$\frac{11}{2}$ЪБЃЌ-$\frac{1}{2}$m+4=$\frac{5}{4}$ЃЌ
ЁрE2ЃЈ$\frac{11}{2}$ЃЌ$\frac{5}{4}$ЃЉЃЛ
ЂлЕБCD=CEЪБЃЌЃЈm-8ЃЉ2+ЃЈ-$\frac{1}{2}$m+4ЃЉ2=25ЃЌНтЕУm4=8+2$\sqrt{5}$ЃЌm5=8-2$\sqrt{5}$ЃЈВЛЗћКЯЬтвтЩсЃЉЃЌ
ЕБm=8+2$\sqrt{5}$ЪБЃЌ-$\frac{1}{2}$m+4=-$\sqrt{5}$ЃЌМДE3ЃЈ8+2$\sqrt{5}$ЃЌ-$\sqrt{5}$ЃЉЃЛ
злЩЯЫљЪіЃКЫљгаЗћКЯЬѕМўЕФЕуEЕФзјБъЮЊE1ЃЈ0ЃЌ-4ЃЉЃЛ E2ЃЈ$\frac{11}{2}$ЃЌ$\frac{5}{4}$ЃЉЃЛE3ЃЈ8+2$\sqrt{5}$ЃЌ-$\sqrt{5}$ЃЉЃЎ
ЃЈ4ЃЉЂйЕБCDЪЧЕШбќШ§НЧаЮЕФЕзЪБЃЌЯпЖЮCDЕФДЙжБЦНЗжЯпгыХзЮяЯпЕФвЛИіНЛЕуМДЮЊPЕуЃЛ
ЂкЕБCPЮЊЕзЪБЃЌвдDЮЊдВаФЃЌвд5ЮЊАыОЖЕФдВгыХзЮяЯпЕФ4ИіНЛЕужаЕФ2ИіЃЈГ§ШЅBЁЂCЕуЃЉМДЮЊЫљЧѓЕФPЕуЃЛ
ЂлЕБPDЮЊЕзЪБЃЌвдCЮЊдВаФЃЌвд5ЮЊАыОЖЕФдВгыХзЮяЯпЕФ2ИіНЛЕуМДЮЊPЕуЃЛ
ЙЪФмЪЙЁїPDCГЦЮЊЕШбќШ§НЧаЮЕФЕуPЕФИіЪ§га5ИіЃЎ
ЙЪД№АИЮЊ5ЃЎ
ЕуЦР БОЬтПМВщСЫЖўДЮКЏЪ§злКЯЬтЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЃЌРћгУЕШбќШ§НЧаЮЕФЖЈвхЕУГіЙигкmЕФЗНГЬЪЧНтЬтЙиМќЃЌвЊЗжРрЬжТлЃЌвдЗРвХТЉЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 40Ёу | BЃЎ | 140Ёу | CЃЎ | 40ЁуКЭ50Ёу | DЃЎ | 40ЁуЛђ140Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 6 | BЃЎ | 7 | CЃЎ | 8 | DЃЎ | 9 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com