
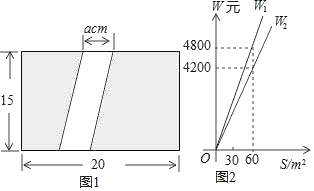
����Ŀ����ͼ1��Ϊ����У������ijУ�ƻ���һ�鳤Ϊ20m����Ϊ15m�ij����οյ�����һ����Ϊa��m�����������µIJ��������ƺ�����̵أ�
��1���������Ϊ�� ��m2���̵ص����Ϊ�� ��m2���ú�a�Ĵ���ʽ��ʾ����
��2����֪ij����˾�������̵ص����W1��Ԫ����W2��Ԫ���������S֮��ĺ�����ϵ��ͼ2��ʾ�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ�� ��Ԫ���� ��Ԫ����ֱ��д�����������W1��Ԫ�������̵ص����W2��Ԫ����a��m���Ĺ�ϵʽ�������ѧУ�����ɸù�˾�н�����Ŀ����Ҫ�����������Ȳ�����2m�Ҳ�����5m����ô����Ϊ����ʱ�����������̵ص��������ͣ���������Ϊ����Ԫ��
���𰸡���1��15a����300��15a������2���٢�80��70������W1��80��15a��1200a��W2��70��300��15a������1050a+21000��������Ϊ2��ʱ�����������̵ص��������ͣ���������Ϊ21300Ԫ��
��������
��1������ͼ�μ�����⣻
��2�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ![]() ��80Ԫ��
��80Ԫ��![]() ��70Ԫ�ڸ������⼴���г���ϵʽ����W��W1+W2��1200a+����1050a+21000����150a+21000���ٸ���2��a��5�����ɽ������.
��70Ԫ�ڸ������⼴���г���ϵʽ����W��W1+W2��1200a+����1050a+21000����150a+21000���ٸ���2��a��5�����ɽ������.
�⣺��1���������Ϊ15am2���̵ص����Ϊ��300��15a��m2��
�ʴ�Ϊ��15a����300��15a����
��2�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ![]() ��80Ԫ��
��80Ԫ��![]() ��70Ԫ��
��70Ԫ��
��W1��80��15a��1200a��
W2��70��300��15a������1050a+21000��
�����������Ŀ���ܷ���ΪWԪ��
��W��W1+W2��1200a+����1050a+21000����150a+21000��
��k��0��
��W��a�����������
��2��a��5��
�൱a��2ʱ��W����Сֵ��W��Сֵ��150��2+21000��21300��
������Ϊ2��ʱ�����������̵ص��������ͣ���������Ϊ21300Ԫ��
�ʴ�Ϊ����80��70��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC=90�㣬D��ֱ��AB�ϵĵ㣬AD=BC��
��1����ͼ1������A��AF��AB����ȡAF=BD������DC��DF��CF���жϡ�CDF����״��֤����
��2����ͼ2��E��ֱ��BC��һ�㣬��CE=BD��ֱ��AE��CD�ཻ�ڵ�P����APD�Ķ�����һ���̶���ֵ�����ǣ���������Ķ����������ǣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ���꼶����12���࣬ÿ��48��ѧ����ѧУ�Ը��꼶ѧ����ѧѧ��ѧҵˮƽ���Գɼ������˳����������밴Ҫ��ش��������⣺
���ռ�������
��1��Ҫ�Ӿ��꼶ѧ���г�ȡһ��48�˵�����������Ϊ���³������������������
________���������ȡһ���༶��48��ѧ�������ھ��꼶ѧ���������ȡ48��Ůѧ����
���ھ��꼶12������ÿ��������ȡ4��ѧ����
���������ݡ�
��2������ȡ��48��ѧ���ijɼ����з��飬���Ƴɼ�Ƶ���ֲ����ͳɼ��ֲ�����ͳ��ͼ���£�
�����ͼ����������գ�
������m��ֵΪ________��
�� B�ಿ�ֵ�Բ�ĽǶ���Ϊ________����
������C��D��ѧ����Լһ����_________����

���꼶ѧ����ѧ�ɼ�Ƶ���ֲ���
�ɼ�����λ���֣� | Ƶ�� | Ƶ�� |
A�ࣨ80��100�� | 24 |
|
B�ࣨ60��79�� | 12 |
|
C�ࣨ40��59�� | 8 | m |
D�ࣨ0��39�� | 4 |
|
���������ݡ�
��3���������ܲ���Ϊ�˽�ѧУѧ���ɼ��������ͬ��εij��ϡ��DZ�������ѧ�ij������ݽ��жԱȷ������õ��±���
ѧУ | ƽ�������֣� | ���� | A��B���Ƶ�ʺ� |
������ѧ | 71 | 358 | 0.75 |
�DZ���ѧ | 71 | 588 | 0.82 |
��������������ѧУѧ����ѧѧҵˮƽ���Եijɼ������һ��������֧����Ĺ۵㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB��90����D��BC���е㣬DE��BC��CE//AD����AC��2��CE��4�����ı���ACEB���ܳ�Ϊ �� ��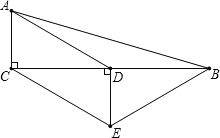
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��a��b�ֱ���������������ͬ��A��B����ʾ������������|a|��5��|b|��2��A��B�����������ϵ�λ����ͼ��ʾ��
![]()
(1)��ȷ����a��b��
(2)A��B���������ٸ���λ���ȣ�
(3)��C���������ϣ�C�㵽B��ľ�����C�㵽A������![]() ����C���ʾ������
����C���ʾ������
(4)��P��A��������������ƶ�1����λ���ȣ��������ƶ�2����λ���ȣ��������ƶ�3����λ���ȣ��������ƶ�4����λ���ȣ����β���2 019�κ���P���ʾ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽���⣮
�����Ӱڳɵ���T������ͼ��ͼ��ʾ��

(1)������
ͼ����� | �� | �� | �� | �� | �� | �� |
ÿ��ͼ�������Ӹ��� | 5 | 8 | �� |
(2)д����n����T������ͼ�������ӵĸ���_________________(�ú�n�Ĵ���ʽ��ʾ)��
(3)��20����T������ͼ����������____________����
(4)����ǰ20����T������ͼ�������ӵ��ܸ�����
(��ʾ��������˼���������⣺��1��ͼ�����20��ͼ���й��ж��ٸ����ӣ���2��ͼ�����19��ͼ���й��ж��ٸ����ӣ���3��ͼ�����18��ͼ���أ�)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��a��0��ͼ����x��Ľ���A��B�ĺ�����ֱ�Ϊ��3��1����y�ύ�ڵ�C�������ĸ����ۣ�
��a��0��ͼ����x��Ľ���A��B�ĺ�����ֱ�Ϊ��3��1����y�ύ�ڵ�C�������ĸ����ۣ�
��16a��4b+c��0������P����5��y1����Q��![]() ��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����a=��
��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����a=��![]() c��������ABC�ǵ��������Σ���b=��
c��������ABC�ǵ��������Σ���b=��![]() ��������ȷ����______���뽫������ȷ�����ȫ�����ϣ�
��������ȷ����______���뽫������ȷ�����ȫ�����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���E�DZ�AC��һ�㣬�߶�BE��ֱ�ڡ�BAC��ƽ�����ڵ�D����MΪ��BC���е㣬����DM��
(1)��֤: DM��![]() CE��
CE��
(2)��AD��6��BD��8��DM��2����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
����1����ѧ����һ�ָ������ִ����ŵ�����������ͨ����ȫƽ��ʽ�����θ�ʽ�����ʻ�ȥһ�㣨���㣩���ţ��磺![]()
![]() ��
��
����2�� �䷽���dz�����ѧ˼�뷽���е�һ����Ҫ�Ľ��ⷽ�����䷽��������Ŀ�ľ��������ȫƽ��ʽ��������ȫƽ��ʽ��������⡣����Ӧ�÷dz��㷺���ڽⷽ�̡�����ֵ��֤����ʽ�������ʽ����ʽ�ֽ�ȷ��涼�����õ���
�磺![]()
��![]() ����
����![]() ��
��![]()
��![]() ����СֵΪ1.
����СֵΪ1.
�������ϲ��Ͻ���������⣺
��1����գ�![]() =________________;
=________________;![]() =______________;
=______________;
��2����![]() ����Сֵ��
����Сֵ��
��3����֪![]() ,��
,��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com