
分析 (1)先根据乘方的法则、绝对值的性质、特殊角的三角函数值及负整数指数幂的计算法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先算括号里面的,再算除法,最后把x的值代入进行计算即可.
解答 解:(1)原式=-4+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-3+2
=-4+1-3+2
=-4;
(2)原式=$\frac{3-{x}^{2}+1}{x+1}$÷$\frac{(x+2)^{2}}{x+1}$
=$\frac{-(x+2)(x-2)}{x+1}$•$\frac{x+1}{(x+2)^{2}}$
=$\frac{2-x}{x+2}$,
当x=$\sqrt{2}$-2时,原式=$\frac{2-\sqrt{2}+2}{\sqrt{2}-2+2}$=2$\sqrt{2}$-1.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连结AC交EF于G,下列结论:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF为等腰直角三角形,其中正确的有①③⑤(填序号).
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连结AC交EF于G,下列结论:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF为等腰直角三角形,其中正确的有①③⑤(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>3 | B. | m≥-3 | C. | m>-3 且m≠-2 | D. | m≤-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
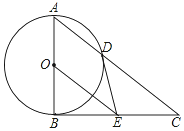 如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.38×105 | B. | 0.238×106 | C. | 23.8×104 | D. | 238×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
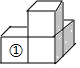 如图,是由4个同样大小的正方体摆成的几何体,将正方体①移走后,关于所得几何体的视图叙述正确的是( )
如图,是由4个同样大小的正方体摆成的几何体,将正方体①移走后,关于所得几何体的视图叙述正确的是( )| A. | 左视图改变 | B. | 主视图不变 | C. | 俯视图改变 | D. | 三视图都不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com