
分析 (1)先利用二次根式的乘法法则运算,然后合并即可;
(2)先把括号内通分,再把除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=2$\sqrt{3×6}$-$\sqrt{\frac{1}{3}×6}$
=6$\sqrt{2}$-$\sqrt{2}$
=5$\sqrt{2}$;
(2)原式=$\frac{(m+2)(m-2)-5}{m-2}$•[-$\frac{2(m-2)}{m-3}$]
=-$\frac{(m+3)(m-3)}{m-2}$•$\frac{2(m-2)}{m-3}$
=-2(m+3)
=-2m-6.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了分式的混合运算.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
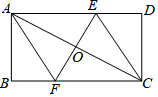 如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正比例函数y1=x的图象与反比例函数y2=$\frac{k}{x}$(k>0)的图象交于A、B两点.
如图,已知正比例函数y1=x的图象与反比例函数y2=$\frac{k}{x}$(k>0)的图象交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com