
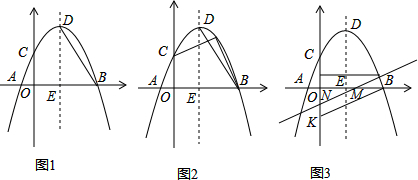
分析 (1)先求出B、D两点的坐标,利用待定系数法求直线BD的解析式;
(2)作辅助线将四边形PBAC的面积分成三部分:两直角三角形和一个直角梯形,设点P的坐标和四边形PBAC的面积为S,利用等量关系列等式,化简后是关于S与m的二次函数,S有最大值即是顶点坐标,求出点P的坐标及直线PC的解析式,并求交点F的坐标,最后求出DF和BF的长和比值;
(3)分二种情况进行讨论:①点M在对称轴的右侧时,设点G(2,y),求直线BK和MN的解析式,并表示出点M和N人坐标;根据△GMN是以MN为直角边的等腰直角三角形得出两直角三角形全等,由对应边相等列方程组可求出b和y的值,写出点G的坐标(2,$\frac{10}{3}$);②点M在对称轴的左侧时,同理可求出点G的坐标为(2,-$\frac{10}{7}$)或(2,-3).
解答 (1)令y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$中y=0,则-$\frac{1}{2}$x2+2x+$\frac{5}{2}$=0,则得x1=-1,x2=5,
∴A(-1,0),B(5,0),
对称轴x=-$\frac{2}{-\frac{1}{2}×2}$=2,
当x=2时,y=-$\frac{1}{2}$×22+2×2+$\frac{5}{2}$=$\frac{9}{2}$,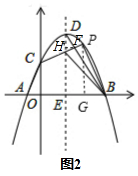
∴D(2,$\frac{9}{2}$),
设直线BD的解析式为y=kx+b(k≠0),把点B(5,0),D(2,$\frac{9}{2}$)代入得:
$\left\{\begin{array}{l}{5k+b=0}\\{2k+b=\frac{9}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{15}{2}}\end{array}\right.$,
∴BD的解析式为y=$-\frac{3}{2}x+\frac{15}{2}$;
(2)如图2所示,过P作PG⊥x轴,垂足为G,
设P(m,-$\frac{1}{2}$m2+2m+$\frac{5}{2}$),四边形PBAC的面积为S,
则S=S△AOC+S梯形OCPG+S△PGB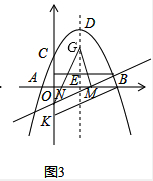
=$\frac{1}{2}$×1×$\frac{5}{2}$+$\frac{1}{2}$×m×($\frac{5}{2}$-$\frac{1}{2}$m2+2m+$\frac{5}{2}$)+$\frac{1}{2}$(5-m)(-$\frac{1}{2}$m2+2m+$\frac{5}{2}$)
=-$\frac{5}{4}$m2+$\frac{25}{4}$m+$\frac{15}{2}$
=-$\frac{5}{4}$(m-$\frac{5}{2}$)2+$\frac{245}{16}$,
∴当m=$\frac{5}{2}$时,S有最大值,
∴-$\frac{1}{2}$m2+2m+$\frac{5}{2}$=-$\frac{1}{2}$×$(\frac{5}{2})^{2}$+2×$\frac{5}{2}$+$\frac{5}{2}$=$\frac{35}{8}$,
∴P($\frac{5}{2}$,$\frac{35}{8}$),
PC的解析式为:y=$\frac{3}{4}$x+$\frac{5}{2}$,
则有$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{5}{2}}\\{y=-\frac{3}{2}x+\frac{15}{2}}\end{array}\right.$ 解得$\left\{\begin{array}{l}{x=\frac{20}{9}}\\{y=\frac{25}{6}}\end{array}\right.$,
∴F($\frac{20}{9}$,$\frac{25}{6}$),
过F作FH⊥对称轴于H,
则DE=$\frac{9}{2}$,DH=$\frac{9}{2}$-$\frac{25}{6}$=$\frac{1}{3}$,
∴DF:BD=DH:DE=$\frac{1}{3}$:$\frac{9}{2}$=2:27;
∴DF:BF=2:25;
(3)①点M在对称轴的右侧时,如图3所示,
直线BK的解析式为:y=$\frac{2}{5}$x-2,
∵BK∥MN,
∴设直线MN的解析式为:y=$\frac{2}{5}$x+b,得M(-$\frac{5}{2}$b,0)、N(0,b),
由已知得MN=MG,∠GMN=90°,
∴∠OMN=∠EGM,∠NOM=∠MEG=90° ,
,
∴△NOM≌△MEG,
设G(2,y),则OM=EG,ON=EM,
∴$\left\{\begin{array}{l}{-\frac{5}{2}b=y}\\{-b=-\frac{5}{2}b-2}\end{array}\right.$ 解得$\left\{\begin{array}{l}{b=-\frac{4}{3}}\\{y=\frac{10}{3}}\end{array}\right.$,
∴G(2,$\frac{10}{3}$);
②当点M在对称轴左侧时,如图4所示,同理得G(2,-$\frac{10}{3}$),
如图5所示,同理得G(2,-3),
综上所述:存在点G的坐标为(2,$\frac{10}{3}$)或(2,-$\frac{10}{3}$)或(2,-3).
点评 本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式,并会用函数的解析式表示图象上某点的坐标,同时把函数和方程相结合,求出点的坐标;并运用了分类讨论的思想,这在函数问题中经常运用,要灵活掌握.


科目:初中数学 来源: 题型:解答题
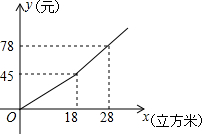 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.| 用水量/立方米 | 水费/元 | |
| 小刚 | 15 | 37.5 |
| 小丽 | 25 | 68.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
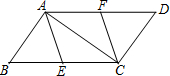 如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,
如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC的中位线DE=10cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是16cm,则△ABC的面积为160cm2.
如图,△ABC的中位线DE=10cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是16cm,则△ABC的面积为160cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com