
分析 首先把原式化成=[${(\sqrt{3}+\sqrt{2})}^{2004}$•($\sqrt{3}$-$\sqrt{2}$)2004]•($\sqrt{3}$-$\sqrt{2}$),再根据平方差公式进行计算,即可得出答案.
解答 解:${(\sqrt{3}+\sqrt{2})}^{2004}$•${(\sqrt{3}-\sqrt{2})}^{2005}$.
=[${(\sqrt{3}+\sqrt{2})}^{2004}$•($\sqrt{3}$-$\sqrt{2}$)2004]•($\sqrt{3}$-$\sqrt{2}$)
=[(3-2)2004]•($\sqrt{3}$-$\sqrt{2}$)
=$\sqrt{3}$-$\sqrt{2}$
点评 本题考查了二次根式的混合运算、平方差公式的运用;熟练掌握平方差公式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
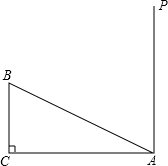 如图,有一个Rt△ABC,∠C=90°,AC=16,BC=8,一条线段MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置,才能使△ABC和△ANM全等.
如图,有一个Rt△ABC,∠C=90°,AC=16,BC=8,一条线段MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置,才能使△ABC和△ANM全等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40cm | B. | 30cm | C. | 20cm | D. | 17cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com