
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,D为AB边上的中点,M,N分别为AC,BC上的点,且DM![]() DN,试说明AB=2(CM+CN)。
DN,试说明AB=2(CM+CN)。

【答案】见解析
【解析】试题分析:(1)根据等腰直角三角形的性质和等腰直角三角形斜边上的中线性质得到∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,再利用等角的余角相等得到∠CDM=∠BDN,然后根据“ASA”可判断△CMD≌△BDN,则CM=BN,又由AC=BC可得AM=CN,即CM+CN=AC=AB,在直角△ABC中AC2+BC2=AB2,即2AC2=AB2,根据等量代换可得:AB=2(CM+CN).
试题解析:
如图,连接CD,
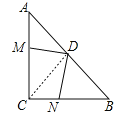
∵△ACB是等腰直角三角形,D为斜边AB的中点,
∴∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,
∴∠CDB=90°,
∵DM⊥DN,
∴∠MDN=90°,
∴∠MDC=∠BDN=90°-∠CDN,
在△CMD和△BND中,
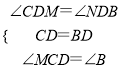 ,
,
∴△CMD≌△BND(ASA),
∴DM=BN,
又∵AC=BC,
∴AM=CN,
∴CM+CN=AC=AB,
在直角△ABC中AC2+BC2=AB2,
∴2AC2=AB2,
∴AB=2(CM+CN).


科目:初中数学 来源: 题型:
【题目】计算:
(1)-2(2x2-xy)-4(x2+xy-1)
(2)69°32′-36°35′
(3)5(a2b﹣3ab2)﹣2(a2b﹣7ab2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷开了一个报亭,为了使每天进的某种报纸适量,王大爷对这种报纸40天的销售情况作了调查,这40天卖出这种报纸的份数如下:136、175、153、135、161、140、155、180、179、166、188、142、144、154、155、157、160、162、135、156、148、173、154、145、158、150、154、168、168、155、169、157、157、149、134、167、151、144、155、131.
将上面数据适当分组,作出频数直方图,说明王大爷每天进多少这种报纸比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.
(1)求证:△AEP≌△BAG;
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2,若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由;
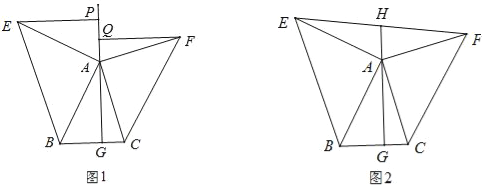
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育》的通知,通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”,“B—了解较多”,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制成以下两幅统计图.

根据以上信息,解答下列问题:
(1)本次抽样调查了多少名学生?
(2)补全两幅统计图;
(3)若该中学共有1 800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
⑴请用代数式表示装饰物的面积:________,用代数式表示窗户能射进阳光的面积是______(结果保留π)
⑵当a=![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )
⑶小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com