
ЁОЬтФПЁПЧыдФЖСЯТСаВФСЯЃК
ЮЪЬтЃКШчЭМ1ЃЌдкЕШБпШ§НЧаЮABCФкгавЛЕуPЃЌЧвPA=2ЃЌPB=![]() ЃЌPC=1ЁЂЧѓЁЯBPCЖШЪ§ЕФДѓаЁКЭЕШБпШ§НЧаЮABCЕФБпГЄЃЎ
ЃЌPC=1ЁЂЧѓЁЯBPCЖШЪ§ЕФДѓаЁКЭЕШБпШ§НЧаЮABCЕФБпГЄЃЎ
РюУїЭЌбЇЕФЫМТЗЪЧЃКНЋЁїBPCШЦЕуBФцЪБеыа§зЊ60ЁуЃЌЛГіа§зЊКѓЕФЭМаЮЃЈШчЭМ2ЃЉЃЌСЌНгPPЁфЃЌПЩЕУЁїPЁфPCЪЧЕШБпШ§НЧаЮЃЌЖјЁїPPЁфAгжЪЧжБНЧШ§НЧаЮЃЈгЩЙДЙЩЖЈРэЕФФцЖЈРэПЩжЄЃЉЃЌДгЖјЕУЕНЁЯBPC=ЁЯAPЁфB=__________ЃЛЃЌНјЖјЧѓГіЕШБпЁїABCЕФБпГЄЮЊ__________ЃЛ
ЮЪЬтЕУЕННтОіЃЎ
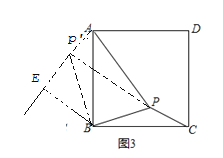
ЧыФуВЮПМРюУїЭЌбЇЕФЫМТЗЃЌЬНОПВЂНтОіЯТСаЮЪЬтЃКШчЭМ3ЃЌдке§ЗНаЮABCDФкгавЛЕуPЃЌЧвPA=![]() ЃЌBP=
ЃЌBP=![]() ЃЌPC=1ЃЎЧѓЁЯBPCЖШЪ§ЕФДѓаЁКЭе§ЗНаЮABCDЕФБпГЄЃЎ
ЃЌPC=1ЃЎЧѓЁЯBPCЖШЪ§ЕФДѓаЁКЭе§ЗНаЮABCDЕФБпГЄЃЎ

ЁОД№АИЁПЃЈ1ЃЉ150ЁуЃЌ![]() ЃЛЃЈ2ЃЉ135ЁуЃЌ
ЃЛЃЈ2ЃЉ135ЁуЃЌ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУа§зЊЕФаджЪЃЌЕУЕНШЋЕШШ§НЧаЮ.
(2)РћгУЃЈ1ЃЉжаЕФНтЬтЫМТЗЃЌАбЁїBPC,а§зЊЃЌЕНЁїBPЁЏA,СЌНгPPЁЏ,BPЁЏЃЌШнвзжЄУїЁїAPPЁЏЪЧжБНЧШ§НЧаЮЃЌЁЯBPЁЏE=45ЁуЃЌвбжЊБпBPЁЏ=BP=![]() ЃЌBE=BPЁЏ=1ЃЌЙДЙЩЖЈРэПЩЧѓЕУе§ЗНаЮБпГЄ.
ЃЌBE=BPЁЏ=1ЃЌЙДЙЩЖЈРэПЩЧѓЕУе§ЗНаЮБпГЄ.
ЃЈ1ЃЉ150Ёу![]()
ЃЈ2ЃЉНЋЁїBPCШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЕУЁїBPЁфAЃЌдђЁїBPCЁеЁїBPЁфAЃЎ
ЁрAPЁф=PC=1ЃЌBP=BPЁф=![]() ЃЛ
ЃЛ
СЌНгPPЁфЃЌдкRtЁїBPЁфPжаЃЌ
ЁпBP=BPЁф=![]() ЃЌЁЯPBPЁф=90ЁуЃЌ
ЃЌЁЯPBPЁф=90ЁуЃЌ
ЁрPPЁф=2ЃЌЁЯBPЁфP=45ЁуЃЛ
дкЁїAPЁфPжаЃЌAPЁф=1ЃЌPPЁф=2ЃЌAP=![]() ЃЌ
ЃЌ
Ёп![]() ЃЌМДAPЁф2+PPЁф2=AP2ЃЛ
ЃЌМДAPЁф2+PPЁф2=AP2ЃЛ
ЁрЁїAPЁфPЪЧжБНЧШ§НЧаЮЃЌМДЁЯAPЁфP=90ЁуЃЌ
ЁрЁЯAPЁфB=135ЁуЃЌ
ЁрЁЯBPC=ЁЯAPЁфB=135ЁуЃЎ
Й§ЕуBзїBEЁЭAPЁфЃЌНЛAPЁфЕФбгГЄЯпгкЕуEЃЛдђЁїBEPЁфЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯEPЁфB=45ЁуЃЌ
ЁрEPЁф=BE=1ЃЌ
ЁрAE=2ЃЛ
ЁрдкRtЁїABEжаЃЌгЩЙДЙЩЖЈРэЃЌЕУAB=![]() ЃЛ
ЃЛ
ЁрЁЯBPC=135ЁуЃЌе§ЗНаЮБпГЄЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫСЫНтШЋаЃЦпФъМЖ300УћбЇЩњЕФЪгСІЧщПіЃЌТцРЯЪІДгжаГщВщСЫ50УћбЇЩњЕФЪгСІЧщПіЁЂеыЖдетИіЮЪЬтЃЌЯТУцЫЕЗЈе§ШЗЕФЪЧ( )
A. 300УћбЇЩњЪЧзмЬхB. УПУћбЇЩњЪЧИіЬх
C. 50УћбЇЩњЕФЪгСІЧщПіЪЧЫљГщШЁЕФвЛИібљБОD. етИібљБОШнСПЪЧ300
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCжаЃЌЁЯAЃН20ЁуЃЌЁЯBЃН70ЁуЃЌФЧУДЁїABCЪЧЃЈЁЁЁЁЃЉ
A. жБНЧШ§НЧаЮ B. ШёНЧШ§НЧаЮ C. ЖлНЧШ§НЧаЮ D. е§Ш§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИїЪНжаМЦЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. t10ЁТt9ЃНt B. ЃЈxy2ЃЉ3ЃНxy6 C. ЃЈa3ЃЉ2ЃНa5 D. x3x3ЃН2x6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжЫЋМчАќЃЌвбжЊетжжЫЋМчАќЕФГЩБОМлЮЊУПИі30дЊЃЎЪаГЁЕїВщЗЂЯжЃЌетжжЫЋМчАќУПЬьЕФЯњЪлСПyЃЈЕЅЮЛ:ИіЃЉгыЯњЪлЕЅМлxЃЈЕЅЮЛ:дЊЃЉгаШчЯТЙиЯЕЃКy=Ѓx+60ЃЈ30ЁмxЁм60ЃЉЃЎ
ЩшетжжЫЋМчАќУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
ЃЈ1ЃЉЧѓwгыxжЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉетжжЫЋМчАќЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉШчЙћЮяМлВПУХЙцЖЈетжжЫЋМчАќЕФЯњЪлЕЅМлВЛИпгк48дЊЃЌИУЩЬЕъЯњЪлетжжЫЋМчАќУПЬьвЊЛёЕУ200дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСадЫЫуе§ШЗЕФЪЧЃЈ ЃЉ
A.m3m3=2m3
B.5m2nЉ4mn2=mn
C.ЃЈm+1ЃЉЃЈmЉ1ЃЉ=m2Љ1
D.ЃЈmЉnЃЉ2=m2Љmn+n2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГИіЙлВтеОВтЕУЃКПеЦјжаpm2.5КЌСПЮЊУПСЂЗНУз0.0000023gЃЌдђНЋ0.0000023гУПЦбЇМЧЪ§ЗЈБэЪОЮЊЃЈЁЁЁЁЃЉ
A. 2.3ЁС10Љ7 B. 2.3ЁС10Љ6 C. 2.3ЁС10Љ5 D. 2.3ЁС10Љ4
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com