
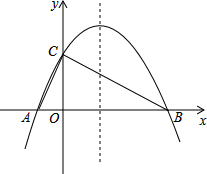
 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).分析 (1)利用待定系数法求出抛物线解析式,利用配方法或利用公式x=-$\frac{b}{2a}$求出对称轴方程;
(2)在抛物线解析式中,令x=0,可求出点C坐标;令y=0,可求出点B坐标.再利用待定系数法求出直线BD的解析式;
(3)本问为存在型问题.若△ACQ为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解.
解答 解:(1)∵抛物线y=-$\frac{1}{4}$x2+bx+4的图象经过点A(-2,0),
∴-$\frac{1}{4}$×(-2)2+b×(-2)+4=0,
解得:b=$\frac{3}{2}$,
∴抛物线解析式为 y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4,
又∵y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=-$\frac{1}{4}$(x-3)2+$\frac{25}{4}$,
∴对称轴方程为:x=3.
(2)在y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4中,令x=0,得y=4,
∴C(0,4);
令y=0,即-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0,整理得x2-6x-16=0,
解得:x=8或x=-2,
∴A(-2,0),B(8,0).
设直线BC的解析式为y=kx+b,
把B(8,0),C(0,4)的坐标分别代入解析式,得:
$\left\{\begin{array}{l}{8k+b=0}\\{b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
∴直线BC的解析式为:y=-$\frac{1}{2}$x+4.
(3)存在,
理由:∵抛物线的对称轴方程为:x=3,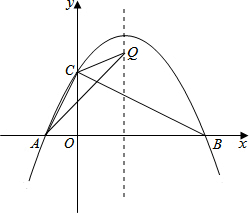
可设点Q(3,t),∵A(-2,0),C(0,4),
∴AC=2$\sqrt{5}$,AQ=$\sqrt{25+{t}^{2}}$,CQ=$\sqrt{(t-4)^{2}+9}$.
①当AQ=CQ时,
有$\sqrt{25+{t}^{2}}$=$\sqrt{(t-4)^{2}+9}$,
25+t2=t2-8t+16+9,
解得t=0,
∴Q1(3,0);
②当AC=AQ时,
有2$\sqrt{5}$=$\sqrt{25+{t}^{2}}$,
∴t2=-5,此方程无实数根,
∴此时△ACQ不能构成等腰三角形;
③当AC=CQ时,
有2$\sqrt{5}$=$\sqrt{(t-4)^{2}+9}$,
整理得:t2-8t+5=0,
解得:t=4±$\sqrt{11}$,
∴点Q坐标为:Q2(3,4+$\sqrt{11}$),Q3(3,4-$\sqrt{11}$).
综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+$\sqrt{11}$),Q3(3,4-$\sqrt{11}$).
点评 此题是二次函数综合题,主要考查了二次函数与一次函数的图象与性质、待定系数法、勾股定理、等腰三角形的判定等知识点.难点在于第(3)问,符合条件的等腰三角形△ACQ可能有多种情形,需要分类讨论.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:解答题
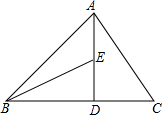 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | 6$\sqrt{2}$+2$\sqrt{3}$ | C. | 6$\sqrt{2}$+4$\sqrt{3}$ | D. | 以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com