
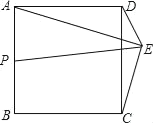
【题目】如图,正方形ABCD的边长为2![]() ,点E为正方形外一个动点,∠AED=45°,P为AB中点,线段PE的最大值是_____.
,点E为正方形外一个动点,∠AED=45°,P为AB中点,线段PE的最大值是_____.
【答案】![]()
【解析】
当点E在正方形右侧时,连接AC,BD交于点O,连接PO,EO,根据A,C,E,D四点共圆,可得OE=OD=![]() ,再根据PE≤OP+OE=
,再根据PE≤OP+OE=![]() ,可得当点O在线段PE上时,PE=OP+OE=
,可得当点O在线段PE上时,PE=OP+OE=![]() ,则线段PE的最大值为
,则线段PE的最大值为![]() ;
;
当点E在正方形上方时,作斜边为AD的等腰直角△AOD,则点E在以O为圆心,OA为半径的圆上,当点P,点O,点E共线时,PE的值最大,求得此时PE最大值为![]() ;比较两个最大值,可得最终结果.
;比较两个最大值,可得最终结果.
解:如图,若点E在正方形右侧,连接AC,BD交于点O,连接PO,EO,
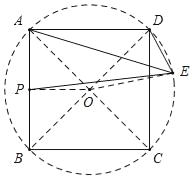
∵∠AED=45°,∠ACD=45°,
∴A,C,E,D四点共圆,
∵正方形ABCD的边长为2![]() ,
,
∴OE=OD=![]() BD=
BD=![]() ,
,
∵P为AB的中点,O是BD的中点,
∴OP=![]() AD=
AD=![]() ,
,
∵PE≤OP+OE=![]() +
+![]() ,
,
∴当点O在线段PE上时,PE=OP+OE=![]() +
+![]() ,
,
即线段PE的最大值为![]() +
+![]() ,
,
如图,点E在正方形ABCD上方,
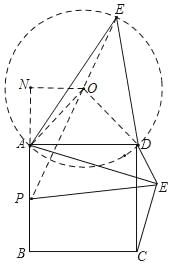
作斜边为AD的等腰直角△AOD,∠AOD=90°,
则点E在以O为圆心,OA为半径的圆上,
∴当点P,点O,点E共线时,PE的值最大,
过点O作ON⊥AB,交BA延长线于点N,
∵AD=2![]() ,AO=DO,∠AOD=90°
,AO=DO,∠AOD=90°
∴AO=![]() ,∠OAD=45°,
,∠OAD=45°,
∵ON⊥AB,AD⊥AB
∴∠NAO=∠NOA=45°
∴AN=NO=![]()
∴PO=![]()
∴PE最大值为![]() ,
,
故答案为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
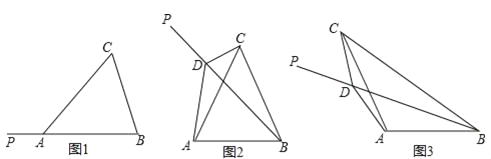
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在开业前,所进三种货物:上衣、裤子和鞋子的数量共480份,这三种货物进货的数量比例如图(1)所示.商店安排6人只销售上衣,4人只销售裤子,2人只销售鞋子,用了5天的时间销售货物的情况如图(2)及表格所示.
(1)求所进三种货物中上衣有多少件?
(2)直接在图中把图(2)补充完整;
(3)表格中的![]() = (直接填空);
= (直接填空);
(4)若销售人员不变,并以同样的销售速度销售,则上衣、裤子和鞋子中最先销售完的货物为 (直接填空).

货物 | 上衣(件) | 裤子(条) | 鞋子(双) |
5天的销售总额 | 150 | a | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可以旋转,当
可以旋转,当![]() 绕点
绕点![]() 逆时针旋转时,投影探头
逆时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到
.(结果精确到![]() )
)
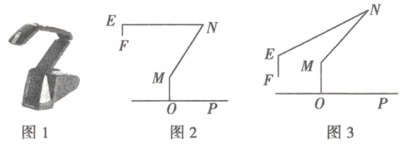
(1)如图2所示,![]() ,
,![]() .
.
①填空:![]() ;
;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离;
的距离;
(2)如图3所示,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据
的大小.(参考数据![]() span>)
span>)
查看答案和解析>>
科目:初中数学 来源: 题型:
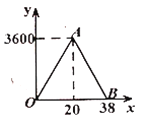
【题目】某校学生食堂共有座位![]() 个,某天午餐时,食堂中学生人数
个,某天午餐时,食堂中学生人数![]() (人)与时间
(人)与时间![]() (分钟)
(分钟)
变化的函数关系图象如图中的折线![]() .
.
(1)试分别求出当![]() 与
与![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)已知该校学生数有![]() 人,考虑到安全因素,学校决定对剩余
人,考虑到安全因素,学校决定对剩余![]() 名同学延时用餐,即等食堂空闲座位不少于
名同学延时用餐,即等食堂空闲座位不少于![]() 个时,再通知剩余
个时,再通知剩余![]() 名同学用餐.请结合图象分析,这
名同学用餐.请结合图象分析,这![]() 名学生至少要延时多少分钟?
名学生至少要延时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为⊙O直径AB延长线上的一点,PC切⊙O于点C,过点B作CP的垂线BH交⊙O于点D,连结AC,CD.
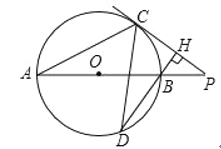
(1)求证:∠PBH=2∠HDC;
(2)若sin∠P=![]() ,BH=3,求BD的长.
,BH=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
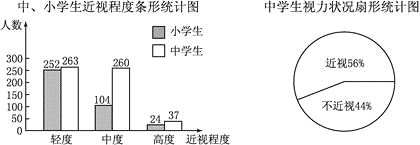
【题目】某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生,对他们的视力状况进行了调查,并把调查结果绘制成如下统计图.(近视程度分为轻度、中度、高度三种)
(1)求这1000名小学生患近视的百分比.
(2)求本次抽查的中学生人数.
(3)该市有中学生8万人,小学生10万人.分别估计该市的中学生与小学生患“中度近视”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克至60千克之间(含20千克和60千克)时,每千克批发5元;若超过60千克是,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:
蔬菜的批发量(千克) | ... | 25 | 60 | 75 | 90 | ... |
所付的金额(元) | ... | 125 | 300 | ... |
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量![]() (千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出
(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
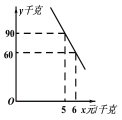
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(5,0),与y轴交于点C(0,![]() ),顶点为D,对称轴交x轴于点E.
),顶点为D,对称轴交x轴于点E.
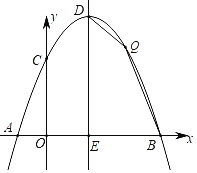
(1)求该抛物线的一般式;
(2)若点Q为该抛物线上第一象限内一动点,且点Q在对称轴DE的右侧,求四边形DEBQ面积的最大值及此时点Q的坐标;
(3)若点P为对称轴DE上异于D,E的动点,过点D作直线PB的垂线交直线PB于点F,交x轴于点G,当△PDG为等腰三角形时,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com