
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЪЧзјБъдЕуЃЌХзЮяЯп
ЪЧзјБъдЕуЃЌХзЮяЯп![]() гы
гы![]() жсе§АыжсНЛгкЕу
жсе§АыжсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.![]() ЃЌЧв
ЃЌЧв![]() ЪМжеБЃГжБп
ЪМжеБЃГжБп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌБп
ЃЌБп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌБп
ЃЌБп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌБп
ЃЌБп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
ЃЈ1ЃЉЬюПеЃЌ![]() ЕФГЄЪЧ ЃЌ
ЕФГЄЪЧ ЃЌ![]() ЕФЖШЪ§ЪЧ ЖШ
ЕФЖШЪ§ЪЧ ЖШ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ЃЌСЌНг
ЃЌСЌНг![]()
ЂйЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЂкХаЖЯЕу![]() ЪЧЗёдкХзЮяЯпЕФЖдГЦжсЩЯЃЌВЂЫЕУїРэгЩЃЛ
ЪЧЗёдкХзЮяЯпЕФЖдГЦжсЩЯЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕББп![]() ОЙ§Еу
ОЙ§Еу![]() ЪБЃЈДЫЪБЕу
ЪБЃЈДЫЪБЕу![]() гыЕу
гыЕу![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() ЃЌНЛ
ЃЌНЛ![]() бгГЄЯпЩЯгкЕу
бгГЄЯпЩЯгкЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕНЕу
ЕНЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌдк
ЃЌдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЈШє
ЃЈШє![]() дкжБЯп
дкжБЯп![]() ЕФЭЌВрЃЉЃЌСЌНг
ЕФЭЌВрЃЉЃЌСЌНг![]() ЃЌЧыжБНгаДГіЕФ
ЃЌЧыжБНгаДГіЕФ![]() ГЄ.
ГЄ.
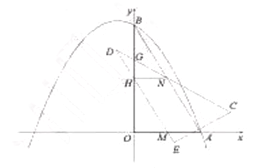
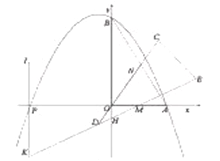
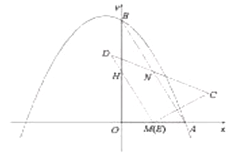
ЁОД№АИЁП(1)8ЃЌ30ЃЛЃЈ2ЃЉЂйЯъМћНтЮіЃЛЂкЕуDдкИУХзЮяЯпЕФЖдГЦжсЩЯЃЌРэгЩЯъМћНтЮіЃЛЃЈ3ЃЉ12![]() .
.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнХзЮяЯпЕФНтЮіЪН![]() ЧѓЕУЕуAЕФзјБъЮЊЃЈ8ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌ8
ЧѓЕУЕуAЕФзјБъЮЊЃЈ8ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌ8![]() ЃЉЃЌМДПЩЕУOA=8,ИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхМДПЩЧѓЕУ
ЃЉЃЌМДПЩЕУOA=8,ИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхМДПЩЧѓЕУ![]() =30ЁуЃЛЃЈ2ЃЉЂйгЩ
=30ЁуЃЛЃЈ2ЃЉЂйгЩ![]() ЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэПЩЕУ
ЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэПЩЕУ![]() ,гжвђOM=AM,ПЩЕУOH=BH,дйгЩBN=ANЃЌИљОнШ§НЧаЮЕФжаЮЛЯпЖЈРэПЩЕУ
,гжвђOM=AM,ПЩЕУOH=BH,дйгЩBN=ANЃЌИљОнШ§НЧаЮЕФжаЮЛЯпЖЈРэПЩЕУ![]() ЃЌМДПЩХаЖЈЫФБпаЮAMHNЪЧЦНааЫФБпаЮЃЛЂкЕуDдкИУХзЮяЯпЕФЖдГЦжсЩЯЃЌШчЭМЃЌЙ§ЕуDзїDR
ЃЌМДПЩХаЖЈЫФБпаЮAMHNЪЧЦНааЫФБпаЮЃЛЂкЕуDдкИУХзЮяЯпЕФЖдГЦжсЩЯЃЌШчЭМЃЌЙ§ЕуDзїDR![]() yжсгкЕуRЃЌгЩ
yжсгкЕуRЃЌгЩ![]() ПЩЕУЁЯNHB=ЁЯAOB=90ЁуЃЌгЩ
ПЩЕУЁЯNHB=ЁЯAOB=90ЁуЃЌгЩ![]() ЃЌПЩЕУЁЯDHB=ЁЯOBA=30ЁуЃЌгжвђ
ЃЌПЩЕУЁЯDHB=ЁЯOBA=30ЁуЃЌгжвђ![]() ЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪПЩЕУЁЯHDG=ЁЯOBA=30ЁуЃЌМДПЩЕУЁЯHDN=ЁЯHNDЃЌЫљвдDH=HN=
ЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪПЩЕУЁЯHDG=ЁЯOBA=30ЁуЃЌМДПЩЕУЁЯHDN=ЁЯHNDЃЌЫљвдDH=HN=![]() OA=4ЃЌдкRtЁїDHRжаЃЌDR=
OA=4ЃЌдкRtЁїDHRжаЃЌDR=![]() DH=
DH=![]() ,МДПЩХаЖЈЕуDЕФКсзјБъЮЊ-2.гжвђХзЮяЯпЕФЖдГЦжсЮЊжБЯп
,МДПЩХаЖЈЕуDЕФКсзјБъЮЊ-2.гжвђХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌЫљвдЕуDдкИУХзЮяЯпЕФЖдГЦжсЩЯЃЛ
ЃЌЫљвдЕуDдкИУХзЮяЯпЕФЖдГЦжсЩЯЃЛ
ЪдЬтНтЮіЃК(1)8ЃЌ30ЃЛ
ЃЈ2ЃЉЂйжЄУїЃКЁп![]() ЃЌ
ЃЌ
Ёр![]() ,
,
гжЁпOM=AM,
ЁрOH=BH,
гжЁпBN=AN
Ёр![]()
ЁрЫФБпаЮAMHNЪЧЦНааЫФБпаЮ
ЂкЕуDдкИУХзЮяЯпЕФЖдГЦжсЩЯЃЌРэгЩШчЯТЃК
ШчЭМЃЌЙ§ЕуDзїDR![]() yжсгкЕуRЃЌ
yжсгкЕуRЃЌ
Ёп![]()
ЁрЁЯNHB=ЁЯAOB=90ЁуЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрЁЯDHB=ЁЯOBA=30ЁуЃЌ
гжЁп![]()
ЁрЁЯHDG=ЁЯOBA=30ЁуЃЌ
ЁрЁЯHDG=ЁЯDHB=30ЁуЃЌ
ЁрЁЯHGN=2ЁЯHDG=60ЁуЃЌ
ЁрЁЯHNG=90Ёу-ЁЯHGN=90Ёу-60Ёу=30ЁуЃЌ
ЁрЁЯHDN=ЁЯHNDЃЌ
ЁрDH=HN=![]() OA=4
OA=4
дкRtЁїDHRжаЃЌDR=![]() DH=
DH=![]() ,
,
ЁрЕуDЕФКсзјБъЮЊ-2.
гжвђХзЮяЯпЕФЖдГЦжсЮЊжБЯп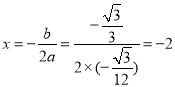 ЃЌ
ЃЌ
ЁрЕуDдкИУХзЮяЯпЕФЖдГЦжсЩЯ.
(3)12![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() АДФцЪБеыЗНЯђа§зЊ
АДФцЪБеыЗНЯђа§зЊ![]() ЃЌЕУЕНЯпЖЮ
ЃЌЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
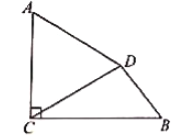
ЃЈ1ЃЉЯпЖЮ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЯпЖЮ![]() ЕФГЄЖШ.
ЕФГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌЕуAЁЂBЕФзјБъЗжБ№ЮЊЃЈ1ЃЌ4ЃЉКЭЃЈ3ЃЌ0ЃЉЃЌЕуCЪЧyжсЩЯЕФвЛИіЖЏЕуЃЌЕБ ![]() зюДѓЪБЃЌЕуCЕФзјБъЪЧ.
зюДѓЪБЃЌЕуCЕФзјБъЪЧ.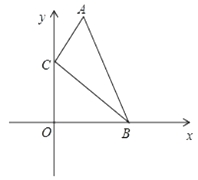
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЧјЕФЕчСІзЪдДЗсИЛЃЌВЂЧвЕУЕНСЫНЯКУЕФПЊЗЂЁЃИУЕиЧјвЛМвЙЉЕчЙЋЫОЮЊСЫЙФРјОгУёгУЕчЃЌВЩгУЗжЖЮМЦЗбЕФЗНЗЈРДМЦЫуЕчЗб. дТгУЕчСПxЃЈЖШЃЉгыЯргІЕчЗбyЃЈдЊЃЉжЎМфЕФКЏЪ§ЭМЯёШчЭМЫљЪО.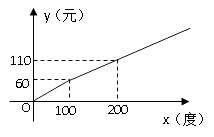
ЃЈ1ЃЉдТгУЕчСПЮЊ100ЖШЪБЃЌгІНЛЕчЗбдЊЃЛ
ЃЈ2ЃЉЕБxЁн100ЪБЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдТгУЕчСПЮЊ260ЖШЪБЃЌгІНЛЕчЗбЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
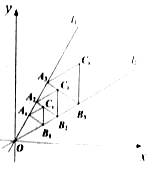
ЁОЬтФПЁПШчЭМЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЙ§Еу
ЩЯЃЌЙ§Еу![]() зї
зї![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЮЊБпдк
ЮЊБпдк![]() ЭтВрзїЕШБпШ§НЧаЮ
ЭтВрзїЕШБпШ§НЧаЮ![]() ЃЌдйЙ§Еу
ЃЌдйЙ§Еу![]() зї
зї![]() ЃЌЗжБ№НЛжБЯп
ЃЌЗжБ№НЛжБЯп![]() КЭ
КЭ![]() гк
гк![]() СНЕуЃЌвд
СНЕуЃЌвд![]() ЮЊБпдк
ЮЊБпдк![]() ЭтВрзїЕШБпШ§НЧаЮ
ЭтВрзїЕШБпШ§НЧаЮ![]() АДДЫЙцТЩНјааЯТШЅЃЌдђЕк
АДДЫЙцТЩНјааЯТШЅЃЌдђЕк![]() ИіЕШБпШ§НЧаЮ
ИіЕШБпШ§НЧаЮ![]() ЕФУцЛ§ЮЊ__________.ЃЈгУКЌ
ЕФУцЛ§ЮЊ__________.ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНјвЛВНСЫНтФГаЃАЫФъМЖбЇЩњЕФЩэЬхЫижЪЧщПіЃЌЬхг§РЯЪІЖдИУаЃАЫФъМЖЃЈ1ЃЉАр50ЮЛбЇЩњНјаавЛЗжжгЬјЩўДЮЪ§ВтЪдЃЌвдВтЪдЪ§ОнЮЊбљБОЃЌЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМЃЌЭМБэШчЯТЫљЪОЃК
зщБ№ | ДЮЪ§x | ЦЕЪ§(ШЫЪ§) |
Ек1зщ | 80ЁмxЃМ100 | 6 |
Ек2зщ | 100ЁмxЃМ120 | 8 |
Ек3зщ | 120ЁмxЃМ140 | a |
Ек4зщ | 140ЁмxЃМ160 | 18 |
Ек5зщ | 160ЁмxЃМ180 | 6 |
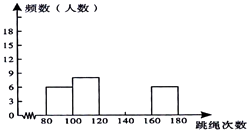
ЧыНсКЯЭМБэЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓБэжаaЕФжЕЃЛ
ЃЈ2ЃЉЧыАбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєдквЛЗжжгФкЬјЩўДЮЪ§Щйгк120ДЮЕФЮЊВтЪдВЛКЯИёЃЌдђИУаЃАЫФъМЖЙВ1000ШЫжаЃЌвЛЗжжгЬјЩў
ВЛКЯИёЕФШЫЪ§ДѓдМгаЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌМзДЌвд16КЃРя/ЪБЕФЫйЖШРыПЊИлПкЃЌЯђЖЋФЯКНааЃЌввДЌдкЭЌЪБЭЌЕиЯђЮїФЯЗНЯђКНааЃЌвбжЊЫћУЧРыПЊИлПквЛИіАыаЁЪБКѓЗжБ№ЕНДяBЁЂAСНЕуЃЌЧвжЊABЃН30КЃРяЃЌЮЪввДЌУПаЁЪБКНааЖрЩйКЃРяЃП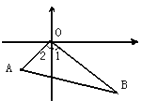
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
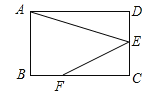
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЕуEЪЧCDЕФжаЕуЃЌЕуFЪЧBCЩЯвЛЕуЃЌЧвFC=2BFЃЌСЌНгAEЃЌEFЃЎШєAB=2ЃЌAD=3ЃЌдђcosЁЯAEFЕФжЕЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com