
【题目】如图,抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 的对称轴交于点
的对称轴交于点![]() ,与
,与![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 的对称轴与
的对称轴与![]() 交于点
交于点![]() .
.
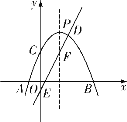
(1)求![]() 的值;
的值;
(2)点![]() 能否与点
能否与点![]() 关于
关于![]() 轴的对称点重合?若认为能,请求出
轴的对称点重合?若认为能,请求出![]() 的值;若认为不能,说明理由;
的值;若认为不能,说明理由;
(3)小林研究了抛物线![]() 的解析式后,得到了如下的结论:因为
的解析式后,得到了如下的结论:因为![]() 可以取任意实数,所以点
可以取任意实数,所以点![]() 可以在
可以在![]() 轴上任意移动,即
轴上任意移动,即![]() 点可以到达
点可以到达![]() 轴的任何位置,你认为他说的有道理吗?说说你的理由;
轴的任何位置,你认为他说的有道理吗?说说你的理由;
(4)当抛物线![]() 与直线
与直线![]() 有两个公共点时,直接写出适合条件的
有两个公共点时,直接写出适合条件的![]() 的最大整数.
的最大整数.
科目:初中数学 来源: 题型:
【题目】2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数![]() (人)与时间
(人)与时间![]() (分钟)的变化情况,数据如下表:(表中9-15表示
(分钟)的变化情况,数据如下表:(表中9-15表示![]() )
)
时间 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9~15 |
人数 | 0 | 170 | 320 | 450 | 560 | 650 | 720 | 770 | 800 | 810 | 810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=9,点P在正方形的边上,则满足PE+PF=8的点P的个数是( )
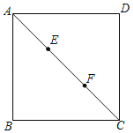
A.8B.6C.4D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.

(1)l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标:
(2)设点C的纵坐标为yc,求yc的最大值,此时l上有两点(x1,y1),(x2,y2),其中x1>x2≥0,比较y1与y1的大小;
(3)当线段OA被l只分为两部分,且这两部分的比是1:4时,求h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
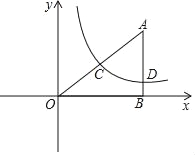
【题目】如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=![]() .
.
(1)若反比例函数y=![]() (x>0)的图象经过AO的中点C,求k的值;
(x>0)的图象经过AO的中点C,求k的值;
(2)在(1)的条件下,若反比例函数y=![]() (x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(3)若点D关于y轴的对称点为E,当反比例函数y=![]() 的图象和线段AE有公共点时,直接写出k的取值范围.
的图象和线段AE有公共点时,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
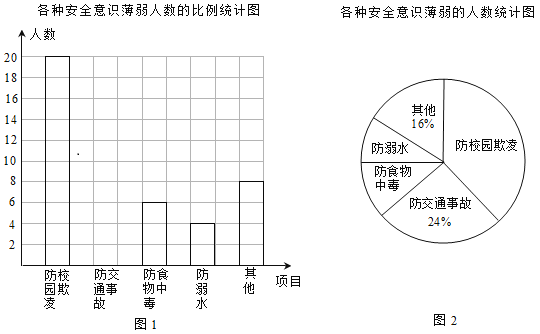
【题目】某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图.
请结合图中的信息解答下列问题:
(1)本次调查的人数为___________,其中防校园欺凌意识薄弱的人数占_________%;
(2)补全条形统计图;
(3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;
(4)请你根据题中的信息,给该校的安全教育提一个合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级一班邀请![]() 、
、![]() 、
、![]() 、
、![]() 、
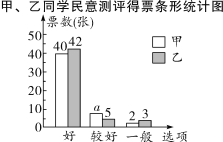
、![]() 五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投票,绘制了如下的打分表和不完整的条形统计图:
五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投票,绘制了如下的打分表和不完整的条形统计图:
五位评委的打分表
A | B | C | D | E | |
甲 | 89 | 91 | 93 | 94 | 86 |
乙 | 88 | 87 | 90 | 98 | 92 |
并求得了五位评委对甲同学才艺表演所打分数的平均分和中位数:
![]() (分);中位数是91分.
(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)![]() ________,并补全条形统计图;
________,并补全条形统计图;
(3)为了从甲、乙两人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:
选拔规则:选拔综合分最高的同学参加艺术节演出.其中,综合分=才艺分![]() 测评分
测评分![]() ;
;
才艺分=五位评委所打分数中去掉一个最高分和一个最低分,再算平均分;测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分
①当![]() 时,通过计算说明应选拔哪位同学去参加艺术节演出?
时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明![]() 的值不能是多少?
的值不能是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形![]() 的边
的边![]() 绕点
绕点![]() 逆时针旋转至
逆时针旋转至![]() ,记旋转角为
,记旋转角为![]() .连接
.连接![]() ,过点
,过点![]() 作
作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,
![]() 如图1,当
如图1,当![]() 时,
时,![]() 的形状为 ,连接
的形状为 ,连接![]() ,可求出
,可求出![]() 的值为 ;
的值为 ;

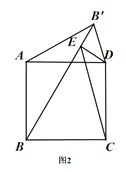
![]() 当
当![]() 且
且![]() 时,
时,
①![]() 中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点![]() 为顶点的四边形是平行四边形时,请直接写出
为顶点的四边形是平行四边形时,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com