
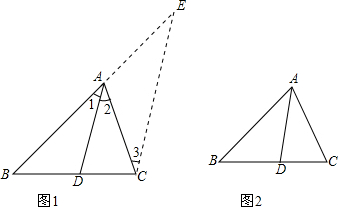
分析 (1)对角平分线定理的证明:过C作CE∥DA,交BA的延长线于E,则根据平行线的性质得到∠1=∠E,∠2=∠3,加上∠1=∠2,则∠E=∠3,于是根据等腰三角形的判定定理得到AE=AC,再证明△BAD∽△BEC,根据相似的性质得$\frac{BD}{BC}$=$\frac{BA}{BE}$,然后用比例得性质易得$\frac{BD}{DC}=\frac{AB}{AC}$;
(2)根据角平分线定理得到$\frac{BD}{DC}=\frac{AB}{AC}$,即$\frac{BD}{7-BD}$=$\frac{5}{4}$,然后利用比例性质求解.
解答  (1)证明:∵CE∥DA,
(1)证明:∵CE∥DA,
∴∠1=∠E,∠2=∠3,
∵AD是角平分线,
∴∠1=∠2,
∴∠E=∠3,
∴AE=AC,
∵CE∥AD,
∴△BAD∽△BEC,
∴$\frac{BD}{BC}$=$\frac{BA}{BE}$,
∴$\frac{BD}{BC-BD}$=$\frac{BA}{BE-BA}$,
∴$\frac{BD}{DC}=\frac{AB}{AC}$;
故答案为等腰三角形的判定定理;相似三角形的性质;
(2)解:∵AD是角平分线,
∴$\frac{BD}{DC}=\frac{AB}{AC}$,即$\frac{BD}{7-BD}$=$\frac{5}{4}$,
∴BD=$\frac{35}{9}$(cm).
点评 本题考查了相似三角形的综合题:熟练掌握相似三角形的判定与性质,会利用相似比计算几何计算;本题证明了角平分线性质定理和此定理的运用.


科目:初中数学 来源: 题型:解答题
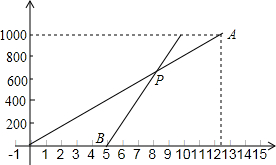 小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:
小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
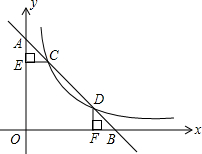 如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.
如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段MP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )| A. | 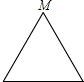 | B. | 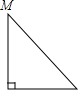 | C. | 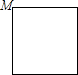 | D. | 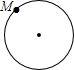 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-7}$ | B. | $\root{3}{2m}$ | C. | $\sqrt{{x^2}+1}$ | D. | $\sqrt{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com