练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．某人的移动电话（手机）可选择两种收费方法中的一种，甲种收费方法是先交月租费50元，每通一分钟电话再收费0.4元；乙种收费方法是不交月租费、每通一分钟电话收费0.6元．问每月通话时间在什么范围内选择甲种收费方法合适？

    分析 设此人每个月的通话时间为x分钟（x≥0），依题意得：甲方案的收费总额：50+0.4x；乙方案的收费总额：0.6x，由题意可得不等式50+0.4x＜0.6x，再解即可．

    解答 解：设此人每个月的通话时间为x分钟（x≥0），依题意得：
    50+0.4x＜0.6x，
    解得：x＞250．
    答：每月通话时间大于250分钟时选择甲种收费方法合适．

    点评 此题主要考查了一元一次不等式的应用，关键是正确理解题意，找出题目中的不等关系，设出未知数，列出不等式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

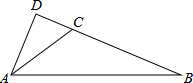    19．如图，在△ABC中，∠ACB=120°，AC=4，BC=6，过点A作BC的垂线，交BC的延长线于点D，则tanB的值为$\frac{\sqrt{3}}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．在等腰三角形中，过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形，我们称这种等腰三角形为“少见的三角形”，这条直线称为分割线，下面我们来研究这类三角形．
    （1）等腰直角三角形是不是“少见的三角形”？
    （2）已知如图所示的钝角三角形是一个“少见的三角形”，请你画出分割线的大致位置，并求出顶角的度数；
    （3）锐角三角形中有没有“少见的三角形”？如果没有，请说明理由；如果有，请画出图形并求出顶角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．在平行四边形ABCD中，BE⊥AD于点E，BF⊥CD于点F，若∠EBF=60°，且AE=2，DF=1，则EC的长为4$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

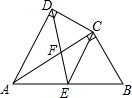    4．如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点．
    （1）求证：CE∥AD；
    （2）若AD=4，AB=6，求CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．△ABC与△DEF在网格中的位置如图所示，如果每个小正方形的边长都是1．
    （1）求$\frac{AB}{DE}$、$\frac{BC}{EF}$、$\frac{AC}{DF}$的值；
    （2）求△ABC的周长与△DEF的周长的比；
    （3）在AB、BC、AC、DE、EF、DF这六条线段中，指出其中三组成比例的线段．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图所示，用不等式表示零件长度的合格尺寸的取值范围是39.8≤L≤40.2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解不等式并在数轴上表示其解集．
    （1）6x＜5x-7；
    （2）2-2x＜x-7；
    （3）0.95x+2.5＞0.9x+10；
    （4）3（x-2）-4（1-x）≤1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，在平面直角坐标系中，直线y=3x+3与x轴、y轴分别交于A、B两点，以AB为边在第二象限作正方形ABCD．将过D点的双曲线y=$\frac{{k}_{1}}{x}$（x＜0）沿y轴对折，得到双曲线y=$\frac{{k}_{2}}{x}$（x＞0），将正方形ABCD沿x轴正方向向右平移a个单位长度后，点C恰好也落在此双曲线y=$\frac{{k}_{2}}{x}$（x＞0）上，则a的值是（　　）
    A．3B．4C．6D．8

    查看答案和解析>>

    同步练习册答案