
【题目】如图,在坐标平面内,已知点A(0,3)、B(6,5),

(1)连接AB,在x轴上确定点P,使PA=PB(用尺规作图,保留作图痕迹,不写作法),并求出P点坐标;
(2)点Q是x轴上的动点,求点Q与A、B两点的距离之和的最小值.
【答案】(1)作图见解析;![]() ;(2)10
;(2)10
【解析】
(1)作线段AB的垂直平分线,与x轴的交点即为点P,此时PA=PB;点P的坐标为(a,0),则OP=a,PD=6﹣a,再利用勾股定理即可求得点P的坐标;
(2)作点A关于x轴的对称点![]() ,连接
,连接![]() ,交x轴于点Q,此时Q与A、B两点的距离之和最小,利用勾股定理即可求得
,交x轴于点Q,此时Q与A、B两点的距离之和最小,利用勾股定理即可求得![]() 的长,即为Q与A、B两点的距离之和的最小值.
的长,即为Q与A、B两点的距离之和的最小值.
(1)如图即为所求:

∵A(0,3)、B(6,5),
∴OA=3,OD=6,BD=5
设点P的坐标为(a,0)
则OP=a,PD=6﹣a
由勾股定理得:![]()
∵AP=BP
![]()
即![]()
解得:![]()
∴点P坐标为![]()
(2)如图,作点A关于x轴的对称点![]() ,连接
,连接![]() ,交x轴于点Q,此时Q与A、B两点的距离之和最小,
,交x轴于点Q,此时Q与A、B两点的距离之和最小,

∵A(0,3)、B(6,5),
∴![]()
由勾股定理得:![]()
∴Q与A、B两点的距离之和最小值为10.


科目:初中数学 来源: 题型:
【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,若MN=2,则NF=___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(﹣3,﹣1),点N的坐标为(3,﹣2).
(1)将线段MN平移得到线段AB,其中点M的对应点为A,点N的对称点为B.
①点M平移到点A的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点B的坐标为 ;
(2)在(1)的条件下,若点C的坐标为(4,0),连接AC,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
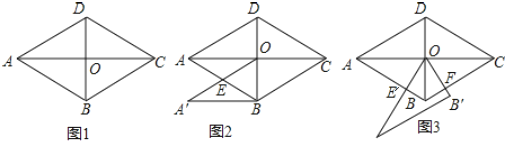
【题目】如图1,菱形ABCD,![]() ,
,![]() ,连接对角线AC、BD交于点O,
,连接对角线AC、BD交于点O,
![]() 如图2,将
如图2,将![]() 沿DB平移,使点D与点O重合,求平移后的
沿DB平移,使点D与点O重合,求平移后的![]() 与菱形ABCD重合部分的面积.
与菱形ABCD重合部分的面积.
![]() 如图3,将
如图3,将![]() 绕点O逆时针旋转交AB于点
绕点O逆时针旋转交AB于点![]() ,交BC于点F,
,交BC于点F,
![]() 求证:
求证:![]() ;
;
![]() 求出四边形
求出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:
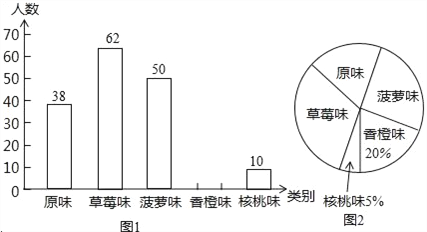
(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com