
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE![]() S菱形ABCD
S菱形ABCD
下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)这条抛物线的对称轴是 , 直线PQ与x轴所夹锐角的度数是;
(2)若两个三角形面积满足S△POQ= ![]() S△PAQ , 求m的值;
S△PAQ , 求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm.bcm,满足(a-3)2+|2a+b-9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D,设运动时间为t s.
(1)a=______cm,b=______cm;
(2)t为何值时,EP把四边形BCDE的周长平分?
(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法,例如:
①用配方法分解因式:![]() .
.
解:原式![]()
②![]() ,利用配方法求
,利用配方法求![]() 的最小值.
的最小值.
解:![]()
∵![]() ,
,![]()
∴当![]() 时,
时,![]() 有最小值1.
有最小值1.
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:![]() ________.
________.
(2)用配方法因式分解:![]() .
.
(3)若![]() ,求
,求![]() 的最小值.
的最小值.
(4)已知![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为选拔参加八年级数学“拓展性课程”活动人选,数学李老师对本班甲、乙两名学生以前经历的10次测验成绩(分)进行了整理、分析(见图①):

(1)写出a,b的值;
(2)如要推选1名学生参加,你推荐谁?请说明你推荐的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
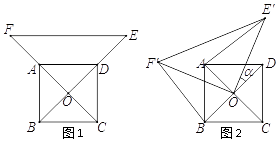
【题目】如图1,已知 ![]() 为正方形
为正方形 ![]() 的中心,分别延长
的中心,分别延长 ![]() 到点
到点 ![]() ,
, ![]() 到点
到点 ![]() ,使
,使 ![]() ,
, ![]() ,连结
,连结 ![]() ,将△
,将△ ![]() 绕点
绕点 ![]() 逆时针旋转
逆时针旋转 ![]() 角得到△
角得到△ ![]() (如图2).连结
(如图2).连结 ![]() 、
、 ![]() .
.
(Ⅰ)探究 ![]() 与
与 ![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当 ![]() ,
, ![]() 时,求:
时,求:
① ![]() 的度数;
的度数;
② ![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于二次三项式 ![]() ,能直接用公式法进行因式分解,得到
,能直接用公式法进行因式分解,得到 ![]() ,但对于二次三项式
,但对于二次三项式 ![]() ,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式
,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式 ![]() 中先加上一项
中先加上一项 ![]() ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 ![]() 这项,使整个式子的值不变,于是:
这项,使整个式子的值不变,于是:

像这样把二次三项式分解因式的方法叫做添(拆)项法.
![]() 问题解决:请用上述方法将二次三项式
问题解决:请用上述方法将二次三项式 ![]() 分解因式.
分解因式.
(2)拓展应用:二次三项式 ![]() 有最小值或有最大值吗?如果有,请你求出来并说明理由.
有最小值或有最大值吗?如果有,请你求出来并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com