
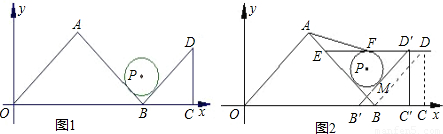
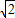 -t,把P点的纵横坐标用t表示出来,从而找出P点的横、纵坐标之间的关系.
-t,把P点的纵横坐标用t表示出来,从而找出P点的横、纵坐标之间的关系.
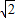 r=
r=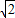 ,OB=
,OB=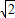 OA=8
OA=8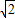 ,
,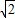 ,纵坐标为
,纵坐标为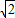 ,则P(8
,则P(8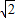 ,
,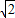 ),
),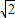 -t,纵坐标为
-t,纵坐标为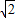 +t,则P(8
+t,则P(8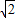 -t,
-t, +t),
+t),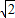 -t+
-t+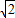 +t=9
+t=9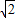 ,所以P点的横、纵坐标之和为定值;
,所以P点的横、纵坐标之和为定值;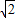 ,B′M=4
,B′M=4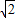 -D′M=3
-D′M=3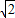 -2,BB′=6-2
-2,BB′=6-2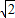 ,
,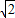 ,得t=3-
,得t=3-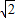 ,
, ×(
×(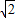 +1)(4
+1)(4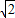 -
-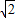 -1-3+
-1-3+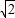 )=2.
)=2.

科目:初中数学 来源:2003年全国中考数学试题汇编《图形的相似》(04)(解析版) 题型:解答题
 .
. ,OE=
,OE=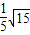 ,求AD:DF的值;
,求AD:DF的值;
查看答案和解析>>
科目:初中数学 来源:2003年湖北省江汉油田中考数学试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2003年湖北省江汉油田中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2003年湖北省江汉油田中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2003年湖北省江汉油田中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com