
����Ŀ��ij��˾Ͷ��1200��Ԫ������һ���������������²�Ʒ�������г����У�����ÿ����Ʒ��Ҫ�ɱ�50Ԫ���ò�Ʒ�����г��õ���80Ԫ/���Ҳ��ó���160Ԫ/�����ò�Ʒ������y����������Ʒ�ۼ�x��Ԫ��֮��Ĺ�ϵ��ͼ��ʾ�� 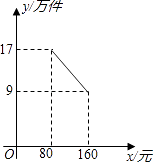
��1����y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2����һ�깫˾��ӯ�����ǿ��������ӯ�����������Сʱ�IJ�Ʒ�ۼۣ�
��3���ڣ�2����ǰ���£����ڵ�һ��ӯ�������߿�����Сʱ����˾�ڶ�������ȷ����Ʒ�ۼۣ��ܷ�ʹǰ����ӯ���ܶ��790��Ԫ�����ܣ�����ڶ����Ʒ�ۼۣ������ܣ�˵�����ɣ�
���𰸡�
��1���⣺��y=kx+b����ͼ��ɵã� ![]() ��
��
��ã� 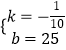 ��
��
����y=�� ![]() x+25��
x+25��
��x��ȡֵ��Χ��80��x��160
��2���⣺��ù�˾��һ�����S��Ԫ����
S=��x��50����y��1200=��x��50������ ![]() x+25����1200
x+25����1200
=�� ![]() x2+30x��2450
x2+30x��2450
=�� ![]() ��x��150��2��200�ܩ�200��
��x��150��2��200�ܩ�200��
���Ե�һ�깫˾�ǿ����ҵ�������Сʱ�IJ�Ʒ�ۼ�Ϊ150Ԫ/��
��3���⣺��������з��̣�x��50������ ![]() x+25��+����200��=790��
x+25��+����200��=790��
��ã�x1=140��x2=160��
����x��ֵ����80��x��160�ڣ�
���Եڶ����ۼ���140Ԫ/����160/��
����������1����y=kx+b������ͼ������k��b���Ӷ��ó�y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ80��x��160����2���蹫˾��һ�����S��Ԫ����ɱ�ʾ��S=�� ![]() ��x��150��2��200�ܩ�200�����һ�깫˾�����ˣ�����Ʒ�ۼ۶�Ϊ150Ԫ/��ʱ��������С����С����Ϊ200��Ԫ����3���������깲ӯ��790��Ԫ����x��50������
��x��150��2��200�ܩ�200�����һ�깫˾�����ˣ�����Ʒ�ۼ۶�Ϊ150Ԫ/��ʱ��������С����С����Ϊ200��Ԫ����3���������깲ӯ��790��Ԫ����x��50������ ![]() x+25��+����200��=790�����x��ֵ��80��x��160�ڣ�
x+25��+����200��=790�����x��ֵ��80��x��160�ڣ�


 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��
��![]() .
.
��1��ͼ�г�ֱ���⣬������ȵĽ�����д�����ԣ����� ������ ����
��2�����![]() �����
�����![]() ����
����![]() ��
��
��3��![]() ��
��![]() ������� ������������ ����
������� ������������ ����
��4�����![]() ����
����![]() �Ķ�����
�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��O��ֱ������C��O�ϣ�����C��ֱ����AB���ӳ��߽��ڵ�P��AC=PC����COB=2��PCB.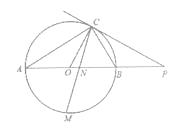
��1����֤��PC��O�����ߣ�
��2����֤��BC= ![]() AB��
AB��
��3����M�ǻ�AB���е㣬CM��AB�ڵ�N����AB=4����MN��MC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д�����������еĹ�ϵʽ����ָ�����еı����ͳ�����
��1��ֱ����������һ�����a����һ�������֮��Ĺ�ϵ��
��2��һʢ��30��ˮ��ˮ�䣬ÿСʱ����0.5��ˮ��������ˮʱ��t��Сʱ����ʾˮ���е�ʣˮ��y���֣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������������ϴ������е�A��B��C������AB=2��BC=1����ͼ��ʾ�����A��B��C����Ӧ���ĺ���p��

��1������BΪԭ�㣬д����A��C����Ӧ������������p��ֵ������CΪԭ�㣬p���Ƕ��٣�
��2����ԭ��O��ͼ�������ϵ�C���ұߣ���CO=28����p��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������չ�Ƽ����»����һ���õ��Գ������С����������50m�����Ļ�У�����������������º������������ڱ���ǰ���н����ϰ�������������ͬʱ��������������������յ�ʱ�������º������յ㻹��2m����֪�����������ƽ���ٶȱ������º�����ƽ���ٶȿ�0.1m/s��
��1���������º�����ƽ���ٶȣ�
��2������������¿�ʼ��ϰ���������������������2m������ͬʱ�����������ܷ�ͬʱ�����յ㣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��1������B��0��1+t����C��0��1��t����t��0������P����D��3��3��ΪԲ�ģ�1Ϊ�뾶��Բ���˶�����ʼ�������BPC=90�㣬��t����Сֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����E��AC���ӳ����ϣ�������������1=��2���ڡ�3=��4���ۡ�A=��DCE���ܡ�D=��DCE���ݡ�A+��ABD=180�㣬�ޡ�A+��ACD=180�����������ж�AB��CD����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬BC=6cm��AC=8cm����P�ӵ�C��ʼ������CA������1cm/s���ٶ��˶���ͬʱ����QҲ�ӵ�C��ʼ������CB������3cm/s���ٶ��˶�.
��1���������PCQ�����Ϊ3cm2����ʱPQ�ij��Ƕ��٣�������������θ�ʽ��ʾ��
��2���������A��B��P��QΪ������ı��ε����Ϊ22cm2��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com