

分析 (1)从条形图可知喜欢剪纸的有100人,根据扇形图可知喜欢剪纸的占总体的20%,从而可求出参与本次调查的人数.
(2)先根据条形图,求得喜爱“葫芦烙画”的人数占调查总人数的百分比,再乘上360°就是其所占的圆心角度数.
(3)先求出喜欢“陶艺”的学生的百分比,再乘以12000就可以估计道外区喜欢“陶艺”的人数.
解答 解:(1)参与本次调查的人数为:100÷20%=500(人);
喜爱“葫芦烙画”的人数为:500-100-220-80=100(人),
条形统计图如图所示: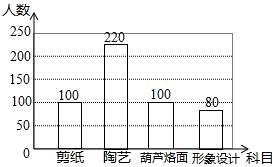
(2)在扇形统计图中,喜爱“葫芦烙画”的人数占调查总人数的百分比为:100÷500=20%,
故“喜爱“葫芦烙画”所对应的扇形的圆心角的度数为:20%×360°=72°;
(3)喜欢“陶艺”的学生占的比例为:220÷500=44%,
故道外区喜欢“陶艺”的人数约有:12000×44%=5280(人).
点评 本题考查学生对条形统计图和扇形统计图的理解能力,解决问题的关键是从图中获得信息,条形统计图给出具体的人数,扇形统计图告诉所占总体的比例.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
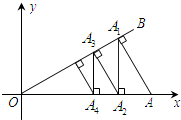 如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;则A2A3=$\frac{3}{4}$;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的纵坐标为$(\frac{\sqrt{3}}{2})^{2017}$.
如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;则A2A3=$\frac{3}{4}$;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的纵坐标为$(\frac{\sqrt{3}}{2})^{2017}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
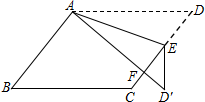 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )| A. | 20° | B. | 30° | C. | 36° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
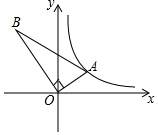 如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | 3 | B. | -3 | C. | -$\frac{9}{2}$ | D. | -$\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com