
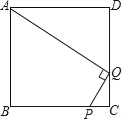
【题目】如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP=_____.
【答案】![]()
【解析】
证明△ADQ∽△QCP:已知的条件有∠C=∠D=90°,那么只要得出另外两组对应角相等即可得出两三角形相似,因为∠DQA+∠CQP=180°-90°=90°,而∠DAQ+∠DQA=90°,因此∠CQP=∠DAQ,那么就构成了两三角形相似的条件;然后由相似三角形的对应边成比例、正方形的四条边都相等及已知条件CQ=1,DQ=2求解即可.
解:∵PQ⊥AQ,
∴∠DQA+∠CQP=180°-90°=90°;
又∵四边形ABCD是正方形,
∴∠DAQ+∠DQA=90°,
∴∠CQP=∠DAQ,
∴ADQ∽△QCP,
![]() ,
,
∵CQ=1,DQ=2,
∴AD=DC=3;
∴CP=![]() ,
,
故答案为:![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形ABCD,其中AD//BC,坡长AB=10cm,坡角![]() ,汛期来临前对其进行了加固,改造后的背水面坡角
,汛期来临前对其进行了加固,改造后的背水面坡角![]() .(注:请在结果中保留根号)
.(注:请在结果中保留根号)
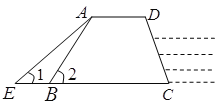
(1)试求出防洪大堤的横断面的高度;
(2)请求出改造后的坡长AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的个数是( )
(1)一个多边形的内角和是外角和的3倍,则这个多边形是六边形;
(2)如果一个三角形的三边长分别为6、8、10,则最长边上的中线长为5;
(3)若△ABC∽△DEF,相似比为1:4,则S△ABC:S△DEF=1:4;
(4)若等腰三角形一个角为80°,则底角为80°或50°.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
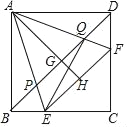
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(2,y1)、B(4,y2)都在反比例函数![]() (k<0)的图象上,则y1、y2的大小关系为( )
(k<0)的图象上,则y1、y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 无法确定
【答案】B
【解析】试题∵当k<0时,y=![]() 在每个象限内,y随x的增大而增大,∴y1<y2,故选B.
在每个象限内,y随x的增大而增大,∴y1<y2,故选B.
考点:反比例函数增减性.
【题型】单选题
【结束】
17
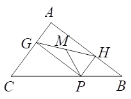
【题目】如图, 在△ABC中,AC=3、AB=4、BC=5, P为BC上一动点,PG⊥AC于点G,PH⊥AB
于点H,M是GH的中点,P在运动过程中PM的最小值为( )
A. 2.4 B. 1.4
C. 1.3 D. 1.2
查看答案和解析>>
科目:初中数学 来源: 题型:
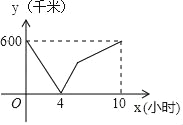
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示:
(1)甲乙两地相距 千米,慢车速度为 千米/小时.
(2)求快车速度是多少?
(3)求从两车相遇到快车到达甲地时y与x之间的函数关系式.
(4)直接写出两车相距300千米时的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“文化宜昌全民阅读”活动中,某中学社团“精一读书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查,2012年全校有1000名学生,2013年全校学生人数比2012年增加10%,2014年全校学生人数比2013年增加100人.
(1)求2014年全校学生人数;
(2)2013年全校学生人均阅读量比2012年多1本,阅读总量比2012年增加1700本(注:阅读总量=人均阅读量×人数)
①求2012年全校学生人均阅读量;
②2012年读书社人均阅读量是全校学生人均阅读量的2.5倍,如果2012年、2014年这两年读书社人均阅读量都比前一年增长一个相同的百分数a,2014年全校学生人均阅读量比2012年增加的百分数也是a,那么2014年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com