
【题目】某公司装修需用A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 2 | M | N |
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m= ,n= ;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?

【答案】(1)m=0,n=3;
(2)y=120﹣![]() x,z=60﹣
x,z=60﹣![]() x;
x;
(3)Q=180﹣![]() x;当x=90时,Q最小,时按三种裁法分别裁90张、75张、0张.
x;当x=90时,Q最小,时按三种裁法分别裁90张、75张、0张.
【解析】
试题(1)按裁法二裁剪时,2块A型板材块的长为120cm,150﹣120=30,所以无法裁出B型板,按裁法三裁剪时,3块B型板材块的长为120cm,120<150,而4块块B型板材块的长为160cm>150所以无法裁出4块B型板;
(2)由题意得:共需用A型板材240块、B型板材180块,又因为满足x+2y=240,2x+3z=180,然后整理即可求出解析式;
(3)由题意,得Q=x+y+z=x+120﹣![]() x+60﹣
x+60﹣![]() x和
x和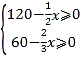 ,[注:事实上,0≤x≤90且x是6的整数倍].由一次函数的性质可知,当x=90时,Q最小.此时按三种裁法分别裁90张、75张、0张.
,[注:事实上,0≤x≤90且x是6的整数倍].由一次函数的性质可知,当x=90时,Q最小.此时按三种裁法分别裁90张、75张、0张.
试题解析:(1)按裁法二裁剪时,2块A型板材块的长为120cm,150﹣120=30,所以无法裁出B型板,
按裁法三裁剪时,3块B型板材块的长为120cm,120<150,
而4块块B型板材块的长为160cm>150cm,所以无法裁出4块B型板;
∴m=0,n=3;
(2)由题意得:共需用A型板材240块、B型板材180块,
又∵满足x+2y=240,2x+3z=180,
∴整理即可求出解析式为:y=120﹣![]() x,z=60﹣
x,z=60﹣![]() x;
x;
(3)由题意,得Q=x+y+z=x+120﹣![]() x+60﹣
x+60﹣![]() x.
x.
整理,得Q=180﹣![]() x.
x.
由题意,得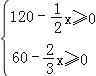
解得x≤90.
[注:事实上,0≤x≤90且x是6的整数倍]
由一次函数的性质可知,当x=90时,Q最小.
由(2)知,y=120﹣![]() x=120﹣
x=120﹣![]() ×90=75,z=60﹣
×90=75,z=60﹣![]() x=60﹣
x=60﹣![]() ×90=0;
×90=0;
故此时按三种裁法分别裁90张、75张、0张.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题. 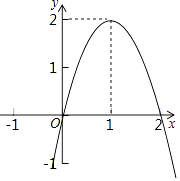
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c=k无实数根,写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | ﹣4 | ﹣4 | 0 | 8 |
(1)根据上表填空; ①方程ax2+bx+c=0的两个根分别是和 .
②抛物线经过点(﹣3,);
③在对称轴左侧,y随x增大而;
(2)求抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费![]() (元)与用水量
(元)与用水量![]() (吨)的函数关系如图所示。
(吨)的函数关系如图所示。
(1)分别写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若某用户该月用水21吨,则应交水费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com