
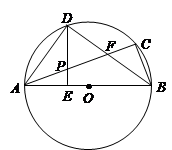
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.

1.求证:∠DAC =∠DBA;
2.求证:![]() 是线段AF的中点
是线段AF的中点
3.若⊙O 的半径为5,AF =![]() ,求tan∠ABF的值.
,求tan∠ABF的值.
1.∵BD平分∠CBA,∴∠CBD=∠DBA
∵∠DAC与∠CBD都是弧CD所对的圆周角,∴![]() ∠DAC=∠CBD
∠DAC=∠CBD
∴![]() ∠DAC =∠DBA (2分)
∠DAC =∠DBA (2分)
2.∵AB为直径,∴∠ADB=90°
又∵DE⊥AB于点E,∴∠DEB=90° ∴∠ADE +∠EDB=∠ABD +∠EDB=90°
∴∠ADE=∠ABD=∠DAP
∴PD=PA
又∵∠DFA +∠DAC=∠ADE +∠PD F=90°且∠ADE=∠DAC
∴∠PDF=∠PFD
∴PD=PF ∴PA= PF 即P是线段AF的中点 (3分)
3.∵∠DAF =∠DBA,∠ADB=∠FDA=90°∴△FDA ∽△ADB
∴![]()
∴在Rt△ABD 中,tan∠ABD= ,即tan∠ABF=
,即tan∠ABF=![]() (3分)
(3分)
解析:(1)根据圆周角定理得出∠DAC=∠CBD,以及∠CBD=∠DBA得出答案即可;
(2)首先得出∠ADB=90,再根据∠DFA+∠DAC=∠ADE+∠PDF=90°,且∠ADB=90°得出∠PDF=∠PFD,从而得出PA=PF;
(3)利用相似三角形的判定得出△FDA∽△ADB即可得出答案.


科目:初中数学 来源: 题型:
 是线段AF的中点
是线段AF的中点 ,求tan∠ABF的值.
,求tan∠ABF的值.查看答案和解析>>
科目:初中数学 来源:2012届江苏苏州九年级中考模拟数学试卷(带解析) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD. 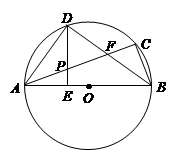
【小题1】求证:∠DAC =∠DBA;
【小题2】求证: 是线段AF的中点
是线段AF的中点
【小题3】若⊙O 的半径为5,AF =  ,求tan∠ABF的值.
,求tan∠ABF的值.
查看答案和解析>>
科目:初中数学 来源:2013届湖北宜城九年级上学期期中考试数学试卷(有解析) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏苏州九年级中考模拟数学试卷(解析版) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
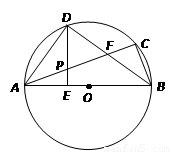
1.求证:∠DAC =∠DBA;
2.求证: 是线段AF的中点
是线段AF的中点
3.若⊙O 的半径为5,AF =
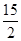 ,求tan∠ABF的值.
,求tan∠ABF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com