【题目】如图，抛物线
与
轴交于点
和点
.（1）已知点
在第一象限的抛物线上，则点
的坐标是_______．（2）在（l）的条件下连接
，
为抛物线上一点且
，则点的坐标是_______．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】定义：几个全等的正多边形依次有一边重合，排成一圈，中间可以围成一个正多边形，我们称作正多边形的环状连接。如图，我们可以看作正六边形的环状连接，中间围成一个边长相等的正六边形；若正八边形作环状连接，中间可以围的正多边形的边数为；
若正八边形作环状连接，中间可以围的正多边形的边数为________，若边长为1的正n边形作环状连接，中间围成的是等边三角形，则这个环状连接的外轮廓长为_________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的限距点的定义如下：若P′为直线PC与⊙C的一个交点，满足r≤PP′≤2r，则称P′为点P关于⊙C的限距点，如图为点P及其关于⊙C的限距点P′的示意图.
(1)当⊙O的半径为1时.
①分别判断点M(3，4)，N(
，0)，T(1，
)关于⊙O的限距点是否存在？若存在，求其坐标；
②点D的坐标为(2，0)，DE，DF分别切⊙O于点E，点F，点P在△DEF的边上.若点P关于⊙O的限距点P′存在，求点P′的横坐标的取值范围；
(2)保持(1)中D，E，F三点不变，点P在△DEF的边上沿E→F→D→E的方向运动，⊙C的圆心C的坐标为(1，0)，半径为r，请从下面两个问题中任选一个作答.
问题1：若点P关于⊙C的限距点P′存在，且P′随点P的运动所形成的路径长为πr，则r的最小值为__________.
问题2：若点P关于⊙C的限距点P′不存在，则r的取值范围为_________.
查看答案和解析>>
科目：初中数学 来源： 题型：
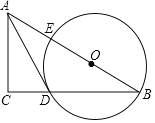
【题目】如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知∠CAD=∠B,
（1）求证：AD是⊙O的切线．
（2）若BC=8，tanB=
，求⊙O 的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD是由三个全等矩形拼成的，AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N，设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3．若S1+S3=30，则S2的值为（ ）．
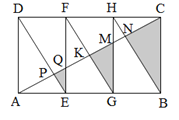
A.6B.8
C.10D.12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线
(
)．
（1）写出抛物线顶点的纵坐标 (用含a的代数式表示)；
（2）若该抛物线与x轴的两个交点分别为点A和点B，且点A在点B的左侧，AB=4．
①求a的值；
②记二次函数图象在点A，B之间的部分为W(含点A和点B)，若直线
(
)经过（1，-1），且与图形W有公共点，结合函数图象，求b的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
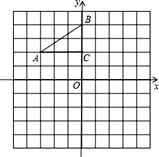
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1，平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；
（2）若将△A1B1C1绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为测量观光塔高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°．已知楼房高AB约是45m，请根据以上观测数据求观光塔的高．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
