
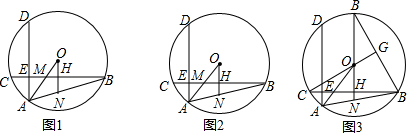
分析 (1)根据OH是BC的中点,即可证明OH⊥BC,并且AD⊥BC,则ON∥AD,根据角平线的性质以及角平分线的定义即可证得;
(2)过点O作OP⊥AD,可证四边形OHEP是矩形,证明△OHM≌△AEM,则OH=AE=$\frac{1}{2}$AP,然后根据垂径定理即可证得;
(3)延长FN交⊙O于点K,连接BK,首先求得∠CBK的度数,然后在直角△OCH中,利用三角函数求得半径的长.
解答 (1)证明:如图1,H是弦BC的中点,
∴AD⊥BC,
∴∠DEB=90°
∴∠OHB=∠DEB,
∴OH∥AD,
∴∠DAO=∠AOH,
∵∠DAO=∠OAN,
∴∠OAN=∠NOA,
∴∠ONB=∠NAO+∠NOA=2∠AON
∴∠ONB=2∠AON;
(2)证明:如图2,过点O作OP⊥AD,可证四边形OHEP是矩形 ,
,
则OH=EP,
∵点M是OA的中点,
在△OHM和△AEM中,
$\left\{\begin{array}{l}{∠OMH=∠AME}\\{OM=AM}\\{∠OHM=∠AEM}\end{array}\right.$,
∴△OHM≌△AEM,
∴OH=AE,
∴EP=AE,
即:AP=2AE=2OH
∵OP⊥AD,
∴AD=2AP,
∴AD=2AP=2×2OH=4OH
∴AD=4OH;
(3)解:如图3,延长FN交⊙O于点K,连接BK,
∵FK是⊙O的直径,
∴∠KBF=90°.
∵CG⊥BF,
∴∠CGF=90°
∴CG∥BK,
∴∠CON=∠OKB.
又∵∠COK=2∠CBK,
∴∠OKB=2∠CBK,
在Rt△HKB中,∠CBK+∠OKB=90°,
∴∠CBK=30°,
∴∠COK=2∠CBK=60°.
在Rt△OCH中,OC=$\frac{CH}{sin60°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∴⊙O的半径为2.
点评 考查了圆的综合题,本题是垂径定理以及全等三角形的判定与性质的综合应用,正确求得∠CBK的度数是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
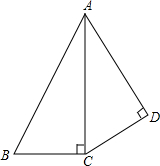 如图,∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以判定△ABC≌△ACD.你认为正确吗?为什么?
如图,∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以判定△ABC≌△ACD.你认为正确吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
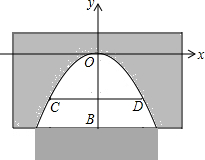 有一座抛物线形拱桥,正常水位时桥下的水深2m,拱顶距水面的距离OB=4m,在如图所示的直角坐标系中,该抛物线的解析式为y=-$\frac{1}{25}$x2,为保证过往船只顺利航行,桥下水面宽度不得小于18m(即CD的长),求水深超过多少米时就会影响过往船只在桥下顺利航行?
有一座抛物线形拱桥,正常水位时桥下的水深2m,拱顶距水面的距离OB=4m,在如图所示的直角坐标系中,该抛物线的解析式为y=-$\frac{1}{25}$x2,为保证过往船只顺利航行,桥下水面宽度不得小于18m(即CD的长),求水深超过多少米时就会影响过往船只在桥下顺利航行?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com