
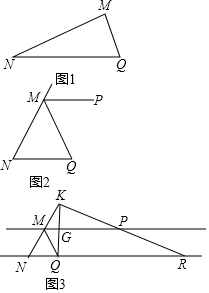
 在三角形MNQ中.
在三角形MNQ中.分析 (1)如图1,作平行线,根据平行线的性质:两直线平行,内错角相等得:∠AMN=∠N,∠BMQ=∠Q,再由平角的定义:∠AMB=180°,等量代换可得结论;
(2)如图2,先由平行线得:∠1=∠N,∠PMQ=∠MQN,再把已知∠PMQ=90°-$\frac{1}{2}$∠NMQ两边同时乘以2,移项得:2∠PMQ+∠NMQ=180°,由平角的定义得:∠1+∠PMQ+∠NMQ=180°,两式对比后得:∠PMQ=∠1,结论得出.
(3)先证明△KQN是直角三角形,并求出NQ的长为9,求△KQN的面积为54,设AN=x,分两种情况:
①当A在点N的左侧时,如图3,AQ=9+x,②当A在点N的右侧时,如图4,AQ=x-9,分别根据△ABQ和△KNQ的面积相等列等式求解.
解答 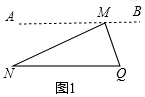 证明:(1)如图1,过M作AB∥NQ,
证明:(1)如图1,过M作AB∥NQ,
∴∠AMN=∠N,∠BMQ=∠Q,
∵∠AMN+∠NMQ+∠BMQ=180°,
∴∠N+∠NMQ+∠Q=180°,
即:∠M+∠N+∠Q=180°;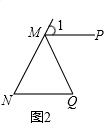
(2)如图2,
∵MP∥NQ,
∴∠1=∠N,∠PMQ=∠MQN,
∵∠PMQ=90°-$\frac{1}{2}$∠NMQ,
∴2∠PMQ=180°-∠NMQ,
∴2∠PMQ+∠NMQ=180°,
∵∠1+∠PMQ+∠NMQ=180°,
∴∠PMQ=∠1,
∴∠N=∠MQN;
(3)∵2KG=KQ,
∴G是KQ的中点,
∵2∠MKG=∠NMQ,∠NMQ=∠MKG+∠MQG,
∴∠MKG=∠MQG,
∴MK=MQ,
∴MG⊥KQ,
∵MP∥NQ,
∴NQ⊥KQ,
∴∠NQK=90°,
∵KN=15,NQ=NR-QR=25-16=9,
∴KQ=$\sqrt{1{5}^{2}-{9}^{2}}$=12,
∴S△KNQ=$\frac{1}{2}$NQ•KQ=$\frac{1}{2}$×9×12=54,
设AN=x,分两种情况:
①当A在点N的左侧时,如图3,AQ=9+x,
∵KQ=12,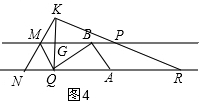
∴GQ=$\frac{1}{2}$KQ=6,
∵S△ABQ=S△KNQ,
∴$\frac{1}{2}$AQ•GQ=54,
$\frac{1}{2}$(9+x)×6=54,
x=9,
②当A在点N的右侧时,如图4,AQ=x-9,
得:$\frac{1}{2}$(x-9)×6=54,
x=27,
则线段AN的长为9或27.
点评 本题是三角形的综合题,难度不大,考查了三角形内角和定理的证明、平行线的性质、等腰三角形的性质和判定等,根据三角形的内角和定理或外角定理可以求角的大小关系,同时与角有关系的性质还有平行线及等腰三角形,都要熟练掌握,在几何证明中经常运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
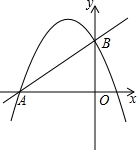 如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且抛物线的对称轴为直线x=-1.
如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且抛物线的对称轴为直线x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
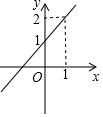 已知:一次函数的图象如图所示.
已知:一次函数的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com