
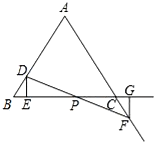
 如图,已知等边△ABC,AB=2,点D在AB上,点F在AC的延长线上,BD=CF,DE⊥BC于E,FG⊥BC于G,DF交BC于点P,则下列结论:①BE=CG;②△EDP≌△GFP;③∠EDP=60°;④EP=1中,一定正确的是①②④.
如图,已知等边△ABC,AB=2,点D在AB上,点F在AC的延长线上,BD=CF,DE⊥BC于E,FG⊥BC于G,DF交BC于点P,则下列结论:①BE=CG;②△EDP≌△GFP;③∠EDP=60°;④EP=1中,一定正确的是①②④. 分析 由等边三角形的性质可以得出△DEB≌△FGC,就可以得出BE=CG,DE=FG,就可以得出△DEP≌△FGP,得出∠EDP=∠GFP,EP=PG,得出PC+BE=PE,就可以得出PE=1,从而得出结论.
解答 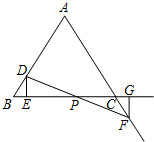 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠ACB=60°.
∵∠ACB=∠GCF,
∵DE⊥BC,FG⊥BC,
∴∠DEB=∠FGC=∠DEP=90°.
在△DEB和△FGC中,
$\left\{\begin{array}{l}{∠DEB=∠FGC}\\{∠GCF=∠A}\\{BD=CF}\end{array}\right.$,
∴△DEB≌△FGC(AAS),
∴BE=CG,DE=FG,故①正确;
在△DEP和△FGP中,
$\left\{\begin{array}{l}{∠DEP=∠FGP}\\{∠DPE=∠FPG}\\{DE=FG}\end{array}\right.$,
∴△DEP≌△FGP(AAS),故②正确;
∴PE=PG∠EDP=∠GFP≠60°,故③错误;
∵PG=PC+CG,
∴PE=PC+BE.
∵PE+PC+BE=2,
∴PE=1,故④正确.
故答案为:①②④.
点评 本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解2016年最新一批炮弹的杀伤半径 | |
| B. | 了解阳泉电视台《XX》栏目的收视率 | |
| C. | 了解黄河的鱼的种类 | |
| D. | 了解某班学生对“山西精神”的知晓率 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (-3,3) | C. | (-3,2) | D. | (0,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 整式包括单项式和多项式 | B. | -m2+n-6是多项式也是整式 | ||
| C. | -m2+n-6的次数为3,常数项为6 | D. | -m2+n-6是二次三项式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com