����⣺��1����y=3x+3��
����y=0�ɵ�x=-1����x=0�ɵ�y=3��
��A����-1��0����B����0��3����
��2����ֱ��m����C��1��0����
��ֱ��m�ķ���Ϊx=1��
��A�����ֱ��x=1�ĶԳƵ�ΪA�䣨3��0����
��ͼ1������A��B��m�ڵ�P����PA+PB=PA��+PB=A��B��С��
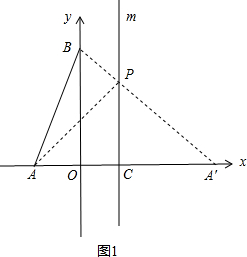
��Rt��OBA���У�OB=3��OA��=3���ɹ��ɶ��������A��B=3
��
��OB=OA�䣬
���PA��C=45�㣬
��PC=CA��=2��
��P��������1��2����
�൱P��Ϊ��1��2��ʱPA+PB����Сֵ3
��
��3����M��������1��y����
���ɹ��ɶ�����֪AB
2=10��AM
2=��1+1��
2+y
2=4+y
2��BM=1
2+��y-3��
2=1+��y-3��
2��
�ߡ�MABΪ���������Σ�
���MA=MB��MB=AB��MA=AB���������
��MA=MBʱ����AM
2=BM
2������4+y
2=1+��y-3��
2�����y=1����ʱM������Ϊ��1��1����
��MB=ABʱ����MB
2=AB
2������10=1+��y-3��
2�����y=0��y=6����ʱMΪ��1��0����1��6����
��MA=ABʱ����MA
2=AB
2������10=4+y
2�����y=
��y=-
����ʱMΪ��1��
����1��-
����
���Ͽ�֪M�������Ϊ��1��1����1��0����1��6����1��
����1��-
����
��4��N���λ����ͼ2��ʾ��
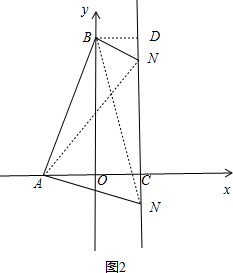
����ABN=90��ʱ����B��BD��m�ڵ�D����N������Ϊ��1��k������BD=OC=1��
�ߡ�ABO+��OBN=��OBN+��DBN=90�㣬
���ABO=��DBN���ҡ�AOB=��BDN��
���ABO�ס�NBD��
��
=
��
��
=
�����DN=
��
��NC=3-
=
��
��ʱN������Ϊ��1��
����
����NAB=90��ʱ��
�ߡ�CAN+��BAO=��BAO+��ABO=90�㣬
���ABO=��CAN���ҡ�AOB=��ACN=90�㣬
��
=
��
��
=
�����CN=
��
��ʱN������Ϊ��1��-
����
��Rt��ACN��AC=2��





 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 ��ͼ����O��ֱ��AB�ϣ�OC�ǡ�AOB��ƽ���ߣ���ֱ��AB����һ���Ե�OΪ��������DOE=90��
��ͼ����O��ֱ��AB�ϣ�OC�ǡ�AOB��ƽ���ߣ���ֱ��AB����һ���Ե�OΪ��������DOE=90��