
分析 (1)由题意分别解出不等式组中的两个不等式,由题意不等式的解集为无解,再根据求不等式组解集的口诀:大大小小找不到(无解)来求出a的范围.
(2)根据分式混合运算的法则把原式进行化简,再题意求出a的值,再代入进行计算即可.
解答 解:(1)由2(x-1)≤a-2,
∴x≤$\frac{1}{2}$a,
由2x-1>0,
∴x>$\frac{1}{2}$,
又关于x的不等式组$\left\{\begin{array}{l}2(x-1)≤a-2\\ 2x-1>0\end{array}\right.$无解,
∴a≤1.
(2)$({\frac{a-1}{{{a^2}-4a+4}}-\frac{a+2}{{{a^2}-2a}}})÷({\frac{4}{a}-1})$
=($\frac{{a}^{2}-a}{a(a-2)^{2}}$-$\frac{{a}^{2}-4}{a(a-2)^{2}}$)÷($\frac{4-a}{a}$)
=$\frac{4-a}{a(a-2)^{2}}$•$\frac{a}{4-a}$
=$\frac{1}{(a-2)^{2}}$,
∵a≤1,a为正整数,
∴a=1,
∴原式=$\frac{1}{(1-2)^{2}}$=1.
点评 主要考查了一元一次不等式组解集的求法,将不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解)逆用,已知不等式解集为无解反过来求a的范围.也考查了分式的化简求值,熟知分式混合运算的法则是解答此题的关键


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
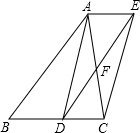 如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.
如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,电信部门要在两条公路之间及海岸线围城的S区域内修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路的距离也必须相等.发射塔P建在什么位置?
如图,电信部门要在两条公路之间及海岸线围城的S区域内修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路的距离也必须相等.发射塔P建在什么位置?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.请证明:四边形EGFH是平行四边形.
如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.请证明:四边形EGFH是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com