
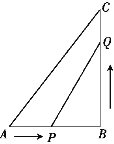
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点P以
,动点P以![]() 的速度从A点出发,沿
的速度从A点出发,沿![]() 向C点移动,同时动点Q以
向C点移动,同时动点Q以![]() 的速度从点C出发,沿
的速度从点C出发,沿![]() 向点B移动,设P、Q两点移动的时间为t秒
向点B移动,设P、Q两点移动的时间为t秒![]() .
.

(1)t为多少时,以P、Q、C为顶点的三角形与![]() 相似?
相似?
(2)在P、Q两点移动过程中,四边形![]() 与
与![]() 的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
【答案】(1)t为![]() 或
或![]() 时,以P、Q、C为顶点的三角形与
时,以P、Q、C为顶点的三角形与![]() 相似;(2)四边形
相似;(2)四边形![]() 与
与![]() 的面积不能相等,理由见解析.
的面积不能相等,理由见解析.
【解析】
(1)先利用勾股定理计算出AC=10,由于∠PCQ=∠ACB,根据三角形相似的判定,当∠PQC=∠B时可判断CQP∽△CBA,利用相似比得到![]() ;当∠PQC=∠BAC时可判断△CQP∽△CAB,利用相似比得到
;当∠PQC=∠BAC时可判断△CQP∽△CAB,利用相似比得到![]() ,然后分别解方程求出t的值即可;
,然后分别解方程求出t的值即可;
(2)作PQ⊥BC于H,如图,先证明△CPH∽△CAB,利用相似比可得到PH=![]() ,再利用四边形ABQP与△CPQ的面积相等得到S△ABC=2S△CPQ,利用三角形面积公式得到2
,再利用四边形ABQP与△CPQ的面积相等得到S△ABC=2S△CPQ,利用三角形面积公式得到2![]() 68,然后解关于t的方程可判断四边形ABQP与△CPQ的面积能否相等.
68,然后解关于t的方程可判断四边形ABQP与△CPQ的面积能否相等.
(1)在R![]() 中,
中,![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ;
;
∴t为![]() 或
或时,以P、Q、C为顶点的三角形与
![]() 相似;
相似;
(2)四边形![]() 与
与![]() 的面积不能相等.
的面积不能相等.
理由如下:
作![]() 于H,如图,
于H,如图,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
当四边形![]() 与
与![]() 的面积相等时,
的面积相等时,
![]() ,即
,即![]() ,
,
∴![]() ,
,
整理得![]() ,此时方程无实数解,
,此时方程无实数解,
∴四边形![]() 与
与![]() 的面积不能相等.
的面积不能相等.



 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);
②运动服的进价是 元/件;当售价是 元/件时,月销利润最大,最大利润是 元.
(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月进馆达到288人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不得超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接待第四个月的进馆人次,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中、点E是BC边上一点,F为AB延长线上一点,且BE=BF,连接AE、EF、CF.
(1)若∠BAE=18°,求∠EFC的度数;
(2)求证:AE⊥CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答下列问题:
阿尔花拉子米(约780~约850),著名阿拉伯数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程x2+2x﹣35=0的一个解.
将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x,宽为1,拼合在一起面积就是x2+2×1+1×1,即x2+2x+1,而由原方程x2+2x﹣35=0变形得x2+2x+1=35+1,即右边边长为x+1的正方形面积为36.所以(x+1)2=36,则x=5.
(1)上述求解过程中所用的方法与下列哪种方法是一致的 .
A.直接开平方法 B.公式法
C.配方法 D.因式分解法
(2)所用的数学思想方法是 .
A.分类讨论思想 B.数形结合思想 C.转化思想
(3)运用上述方法构造出符合方程x2+4x﹣5=0的一个正根的正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,同时点Q从点B开始沿BC向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,运动时间为x秒(x>0).
(1)求几秒后,PQ的长度等于5 cm.
(2)运动过程中,△PQB的面积能否等于8 cm2?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()
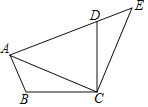
A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com