【题目】从﹣3、﹣1、 
、1、3这五个数中，随机抽取一个数，记为a，则关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为 ．
【答案】
【解析】解：当a=﹣3，则y=﹣x﹣3，此时图象与x轴交点为：（﹣3，0），与y轴交点为：（0，﹣3），
故一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为4.5，不合题意；
当a=3，则y=﹣x+3，此时图象与x轴交点为：（3，0），与y轴交点为：（0，3），
故一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为4.5，不合题意；
当a=﹣1、 
、1时，一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为： ， 
，符合题意，
故关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为： ．
所以答案是： ．
【考点精析】本题主要考查了概率公式的相关知识点，需要掌握一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n才能正确解答此题．
新思维假期作业寒假吉林大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．
（1）试说明AC=EF；
（2）求证：四边形ADFE是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD顶点A、B在x轴上，点D在y轴上，函数y= 
（x＞0）的图象经过点C（2，3），直线AD交双曲线于点E，并且EB⊥x轴，CD⊥y轴，EB与CD交于点F．
（1）若EB= 
OD，求点E的坐标；
（2）若四边形ABCD为平行四边形，求过A、D两点的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，∠BAC=30°，点D是△ABC内一点，DB=DC，∠DCB=30°，点E是BD延长线上一点，AE=AB．
（1）求∠ADE的度数；
（2）求证：DE=AD+DC；
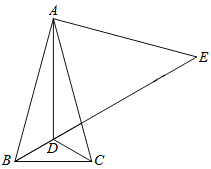
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线MN与x轴、y轴分别相交于B、A两点，OA,OB的长满足式子
(1)求A，B两点的坐标;
(2)若点O到AB的距离为
，求线段AB的长；
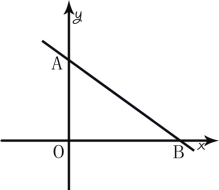
（3）在（2）的条件下，x轴上是否存在点P,使ΔABP使以AB为腰的等腰三角形，若存在请直接写出满足条件的点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.为了了解全国中学生每天体育锻炼的时间，应采用普查的方式
B.若甲组数据的方差s 
=0.03，乙组数据的方差是s 
=0.2，则乙组数据比甲组数据稳定
C.广安市明天一定会下雨
D.一组数据4、5、6、5、2、8的众数是5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点
，点
，其中
，
，点
是
轴负半轴上一点，点
是在直线
与直线
之间的一点，连接
、
，
平分
，
平分
，交于
，则
与
之间可满足的数量关系式为______________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】由甲、乙两个工程队承包某校校园绿化工程，甲、乙两队单独完成这项工程所需时间比是3︰2，两队合做6天可以完成．
（1）求两队单独完成此项工程各需多少天?
（2）此项工程由甲、乙两队合做6天完成任务后，学校付给他们20000元报酬，若
按各自完成的工程量分配这笔钱，问甲、乙两队各得到多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
