
分析 (1)找出a,b及c,表示出根的判别式,变形后得到其值大于0,即可得证;
(2)利用因式分解法求得方程的两个根,结合方程的根是整数、m是整数进行解答;
(3)设二次函数的图象向下平移2个单位,若其与x轴的一个交点为(x1,0),(x2,0),根据交点在(3,0)和(4,0)之间,于是得到$\left\{\begin{array}{l}{(3-{x}_{1})({x}_{2}-3)>0}\\{(4-{x}_{1})(4{-x}_{2})>0}\end{array}\right.$或$\left\{\begin{array}{l}{{(x}_{1}-3)({x}_{2}-3)>0}\\{(4-{x}_{1})({x}_{2}-4)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{6-2m}{m}>0}\\{\frac{6m-8}{m}>0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{2m-6}{m}>0}\\{\frac{-6m-8}{m}>0}\end{array}\right.$解不等式组即可得到结果.
解答 (1)证明:△=b2-4ac=(3m+2)2-4m(2m+2)=(m+2)2,
∵m>0,(m+2)2>0,即△>0,
∴方程总有两个不相等的实数根;
(2)∵mx2-(3m+2)x+2m+2=(x-1)(mx-2m-2)=0,
∴x1=1,x2=2+$\frac{2}{m}$,
∵方程的根都为整数,
∴m=1,或2;
(3)设二次函数的图象向下平移2个单位,若其与x轴的一个交点为(x1,0),(x2,0),
∵交点在(3,0)和(4,0)之间,
∴$\left\{\begin{array}{l}{(3-{x}_{1})({x}_{2}-3)>0}\\{(4-{x}_{1})(4{-x}_{2})>0}\end{array}\right.$或$\left\{\begin{array}{l}{{(x}_{1}-3)({x}_{2}-3)>0}\\{(4-{x}_{1})({x}_{2}-4)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{6-2m}{m}>0}\\{\frac{6m-8}{m}>0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{2m-6}{m}>0}\\{\frac{-6m-8}{m}>0}\end{array}\right.$
解得:$-\frac{4}{3}$<m<3,
∴m的取值范围是:$-\frac{4}{3}$<m<3.
点评 本题考查一元二次方程根的判别式、二次函数的图象及函数图象的平移,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了根与系数的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
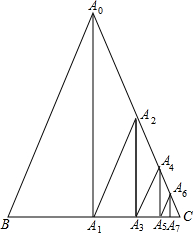 如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )
如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )| A. | $\frac{5}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{96}$ | D. | $\frac{5}{128}$ |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
已知:如图,AB∥CD,∠1=∠2,求证:∠B=∠D.
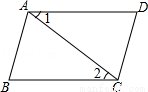
证明:∵∠1=∠2(已知)
∴ ∥ ( )
∴∠BAD+∠B=180°( )
又∵AB∥CD(已知)
∴ + =180°( )
∴∠B=∠D( )
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com