
【题目】如图,点O为直线AB上一点,∠AOC=48°,OD平分∠AOC,OE⊥OD交于点O.
(1)求出∠BOD的度数;
(2)试用计算说明∠COE=∠BOE.

【答案】(1)∠BOD=156°;(2)见解析
【解析】
(1)由角平分线的性质即可推出![]() ,然后根据邻补角的性质即可推出
,然后根据邻补角的性质即可推出![]() 的度数;
的度数;
(2)首先根据垂线的性质和(1)所得的结论,即可推出![]() 和
和![]() 的度数,然后根据角平分线的定义即可确定
的度数,然后根据角平分线的定义即可确定![]() 平分
平分![]() .
.
解:(1)∵OD平分∠AOC
∴∠AOD=∠DOC=![]() ∠AOC=
∠AOC=![]() ×48°=24°,
×48°=24°,
∴∠BOD=180°﹣∠AOD=180°﹣24°=156°;
(2)∵OE⊥OD,
∴∠DOE=90°,
∵∠DOC=24°,
∴∠COE=∠DOE﹣∠DOC=90°﹣24°=66°,
∵∠BOD=156°,∠DOE=90°,
∴∠BOE=∠BOD﹣∠DOE=156°﹣90°=66°,
∴∠COE=∠BOE.


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架云梯长25 m,斜靠在一面墙上,梯子靠墙的一端距地面24 m.
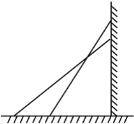
(1)这个梯子底端离墙有多少米?
(2) 如果梯子的顶端下滑了4m,那么梯子的底部在水平方向也滑动了4m吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
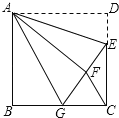
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为OB上的一点,按下列要求进行尺规作图(保留作图痕迹),并回答问题.
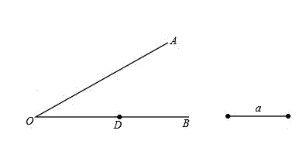
(1)作∠AOB的平分线OC,在OC上取一点P使得OP=a;
(2)过点P作OA边上的高;
(3)在边OA上取一点E,使得PE=PD,请写出∠OEP与∠ODP的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)![]() ;
;
(9)![]() ;
;
(10)![]() ;
;
(11)20032;
(12)![]() ;
;
(13)![]() ;
;
(14)![]() ;
;
(15)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
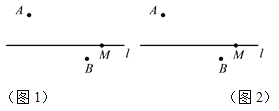
【题目】作图题:已知点A,点B,直线l及l上一点M.
(1)如图1,连接MA,并在直线l上作出一点N,使得点N在点M的左边,且满足MN=MA,作线段MN的中点C,连接BC;
(2)如图2,请在直线l上确定一点O,使点O到点A与点O到点B的距离之和最短,并写出画图的依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
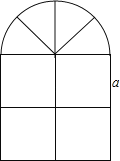
【题目】窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com