
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.动点P,Q同时从点C出发,均以1cm/s的速度运动,其中点P沿CA向终点A运动;点Q沿CB向终点B运动.过点P作PE∥BC,分别交AD,AB于点E,F,设动点Q运动的时间为t秒.
(1)求DQ的长(用含t的代数式表示);
(2)以点Q,D,F,E为顶点围成的图形面积为S,求S与t之间的函数关系式;
(3)连接PQ,若点M为PQ中点,在整个运动过程中,直接写出点M运动的路径长.

【答案】(1)当0≤t≤3时,DQ=3﹣t;当3<t≤5时,DQ=t﹣3.
(2) ;
;
(3)3![]() .
.
【解析】
(1)由于CD=3cm,运动速度为1m/s,故进行分类讨论,分别为当0≤t≤3时,当3<t≤5时,分别计算出DQ的长度即可.
(2)根据梯形面积公式和三角形面积公式,分类进行讨论,分别当0≤t≤3时和当3<t≤4时,四点围成的是一个梯形,当4<t≤5时,E、F点重合,此时围成的是一个三角形.分别计算,用含t的式子将S表示出来即可.
(3)根据题意,CB>CA,故M点的运动轨迹分为两段,一段为P点运行到A点,Q点运行到与CA的长相等的地方可设为J点,此时M运行的路经长为等腰直角△JCA的底边的垂线CR,第二段,过R点作BC的平行线,与AB交于点T,此时P点已经停止在了A点,Q点继续由J点向B点运动,此时M点的运行轨迹即为RT的长,分别计算出两段的长,相加即可.
解:(1)当0≤t≤3时,DQ=CD-CQ
∵CD=3,CQ=t,
∴DQ =3﹣t;
当3<t≤5时,DQ=CQ-CD
∵CQ =t,CD =3,
∴DQ =t﹣3.
(2)①当0≤t≤3时,如图,
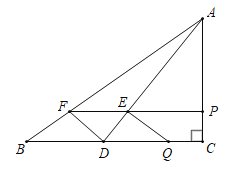
∵PC=t,AC=4,
∴![]() ,
,
![]()
![]() ,
,
![]() ,
,
∴![]() .
.
②当3<t≤4时,如图,
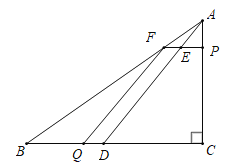
∴![]() .
.
③当4<t≤5时,如图,
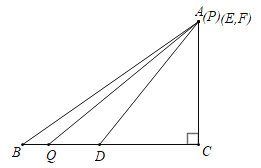
∴![]() .
.
综上所述
(3)点M运动的路径长为2![]() ,
,
如图,在CB上取一点J,使得CJ=CA,连接AJ,作CR⊥AJ于R,RT∥BC交AB于T.
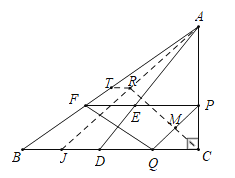
由题意点M的运动路径是C→R→T,
∵CA=CJ=4,CR⊥AJ,∠ACJ=90°,
∴AJ=4![]() ,AR=RJ,
,AR=RJ,
∴CR=![]() AJ=2
AJ=2![]() ,
,
∵RT∥BJ,AR=RJ,
∴AT=TB,
∴RT=![]() BJ=
BJ=![]() ,
,
∴点M的运动路径的长为2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
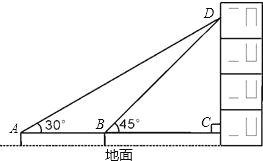
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等腰![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、点
、点![]() .
.
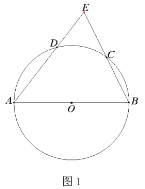
(1)如图1,求证:点![]() 为弧
为弧![]() 的中点;
的中点;
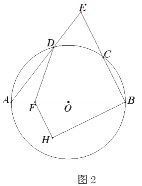
(2)如图2,点![]() 为直径
为直径![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交过点
,交过点![]() 且垂直于
且垂直于![]() 的直线于点
的直线于点![]() ,连接
,连接![]() ,
,![]() ,设
,设![]()
![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
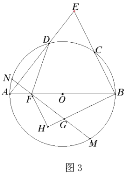
(3)如图3,在(2)的条件下,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]()
![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
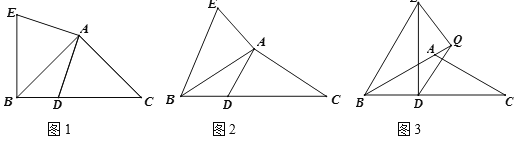
【题目】△ABC中,∠BAC=α°,AB=AC,D是BC上一点,将AD绕点A顺时针旋转α°,得到线段AE,连接BE.
(1)(特例感知)如图1,若α=90,则BD+BE与AB的数量关系是 .
(2)(类比探究)如图2,若α=120,试探究BD+BE与AB的数量关系,并证明.
(3)(拓展延伸)如图3,若α=120,AB=AC=4,BD=![]() ,Q为BA延长线上的一点,将QD绕点Q顺时针旋转120°,得到线段QE,DE⊥BC,求AQ的长.
,Q为BA延长线上的一点,将QD绕点Q顺时针旋转120°,得到线段QE,DE⊥BC,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
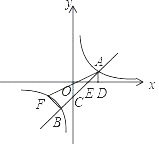
【题目】如图,A,B为反比例函数y=![]() 图象上的点,AD⊥x轴于点D,直线AB分别交x轴,y轴于点E,C,CO=OE=ED.
图象上的点,AD⊥x轴于点D,直线AB分别交x轴,y轴于点E,C,CO=OE=ED.
(1)求直线AB的函数解析式;
(2)F为点A关于原点的对称点,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
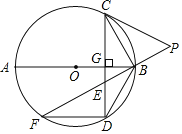
【题目】如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连接CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.
(1)连结BC,求证:△BCD≌△DFB;
(2)求证:PC是⊙O的切线;
(3)若tanF=![]() ,AG﹣BG=
,AG﹣BG=![]() ,求ED的值.
,求ED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘 ![]() ,记为
,记为![]() .如
.如![]() ,此时,
,此时,![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).一般地,若
).一般地,若![]() ,(
,(![]() 且
且![]() ,
,![]() ),则
),则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).如
).如![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).
).
(1)计算以下各对数的值:![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(2)观察(1)中三数![]() 、
、![]() ,
,![]() 之间满足怎样的关系式,
之间满足怎样的关系式,![]() 、
、![]() 、
、![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?![]() __________.(
__________.(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根据幂的运算法则:![]() 以及对数的含义证明上述结论.
以及对数的含义证明上述结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com