如图.光源P在水平放置的横杆AB的正上方.AB在灯光下的影子CD也呈水平状态.AB=2m.CD=6m.点P到CD的距离是3.9m.则AB与CD之间的距离是( )A．2.6mB．2mC．1.3mD．1m 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

17．

如图，光源P在水平放置的横杆AB的正上方，AB在灯光下的影子CD也呈水平状态，AB=2m，CD=6m，点P到CD的距离是3.9m，则AB与CD之间的距离是（　　）

A．

2.6m

B．

C．

1.3m

D．

分析易得△PAB∽△PCD，利用相似三角形对应边的比等于对应高的比可得AB与CD间的距离．

解答解：如图，作PF⊥CD于点F，
∵AB∥CD，
∴△PAB∽△PCD，PE⊥AB，
∴△PAB∽△PCD，
∴$\frac{AB}{CD}$=$\frac{PE}{PF}$，
$\frac{2}{6}$=$\frac{3.9-EF}{3.9}$，
解得EF=2.6．
故选：A．

点评考查相似三角形的应用；用到的知识点为：相似三角形对应边的比等于对应高的比．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

7．已知两圆的半径半径分别是3和2，圆心的坐标分别是（3，0）和（0，-4），那么两圆的位置关系是（　　）

A．

外切

B．

相交

C．

内切

D．

外离

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

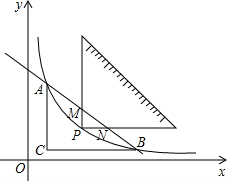如图，将一块直角三角形纸板的直角顶点放在C（1，$\frac{1}{2}$）处，两直角边分别与x，y轴平行，纸板的另两个顶点A，B恰好是直线y=kx+b与双曲线y=$\frac{4}{x}$的交点．
（1）求k和b的值；
（2）设双曲线y=$\frac{4}{x}$在A，B之间的部分为L，让一把含45°的三角尺的直角顶点P在L上滑动，两直角边始终与坐标轴平行，且与线段AB交于M，N两点，请探究是否存在点P使得MN=$\frac{1}{2}$AB，写出你的探究过程和结论；
（3）在（2）的条件下，△MPN 的面积是否存在最大值？若有，请求出面积最大值及点P的坐标；若没有，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

5．在计数制中，通常我们使用的是“十进位制”，即“逢十进一”，而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据．已知二进位制与十进位制的比较如表：

十进位制	0	1	2	3	4	5	6	…
二进位制	0	1	10	11	100	101	110	…

请将二进位制数1010101_（2）写成十进位制数是（　　）

A．

B．

C．

170

D．

171

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．阅读材料：本册数学学习中，我们认识了“完全平方公式”，即（a±b）²=a²±2ab+b²，并把形如a²±2ab+b²的式子称为完全平方式．
把形如ax²+bx+c（a≠0）的二次三项式（或其一部分）配成完全平方式的过程叫配方．配方的基本形式是完全平方公式的逆写，即a²±2ab+b²=（a±b）²．例如
①选取二次项和一次项配方：x²-2x+4=（x-1）²+3；
②选取二次项和常数项配方：x²-2x+4=（x+2）²-6x，
或x²-2x+4=（x-2）²+2x；
③选取一次项和常数项配方：x²-2x+4=（$\frac{1}{2}$x-2）²+$\frac{3}{4}$x²．
根据上述材料，解决下面问题：
（1）写出x²+4x+9的两种不同形式的配方；
（2）已知4x²+y²-4x+6y+10=0，求x^y的值；
（3）试求当x为何值时，-x²+4x+5有最大值，最大值是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：选择题